DLP and TLP

Types of Vector Architectures¶

主要有两种：

Memory-memory vector processor: 没有 register 或者 cache，读写都是直接往 memory 中，不过 memory load/store module 会有流水线
Cache-register vector processor: 还是有 register 以及 cache

目前来说，主要还是用第二种。

Components of a Vector Processor¶

组成有三点：

Vector Register: 这些 register 的宽度很大。假设一个标准 register 的宽度是 64 bits (8 bytes)，那么这些 vector 可能有 512 B 甚至 1 KiB 大小（也就是 64~128 个标准寄存器宽度）。一个支持向量化的 CPU 里面，可能会有 8~32 个这样的 vector 寄存器
Vector Function Unit: Fully pipelined, start new operation every clock
- Typically 4 to 8 FUs
  - FP add
  - FP mult
  - FP reciprocal (1/X)
  - integer add, logical, shift
- may have multiple of same unit
Vector Load-Store Units: Multiple elements fetched/stored per cycle
- may have multiple LSUs
Scalar registers: single element for FP scalar or address

优缺点

Basic Vector Instructions¶

指令并不多，实现也简单（不需要检测指令内部的冲突，因为没有冲突）；至于指令之间，我们只要能检测出结构冲突、指令冲突即可。并不需要做太多优化。

三种寻址方式，从上到下越来越慢。可以类比 numpy 中的三种情况：

v1 = a[0,:] # Unit stride: Get the 0-th row
v2 = a[:, 0] # Non-unit stride: Get the 0-th column
v3 = a[np.arange(a.shape[0]), np.abs(a).argmax(dim=1)] # Indexed: Get the value of each row that has the maximum absolute value
## Note: `dim = 1` means that the argmax is ALONG dim = 1 (column), thus staying at the same dim = 0 (row).

例子¶

Problem: 向量长度¶

如果需要进行运算的长度超过了向量长度怎么办？我们可以进行多次迭代（每一次迭代都是向量相加）。

最后除不尽，有剩余怎么办（比如需要进行 1000 个 unsigned long long 的相加，最长向量长度是 64，那么进行 15 次迭代之后，只处理了 960 个 ULL，还有 40 个剩余）？可以调整向量长度，因为向量长度 can be anything from 0 to MVL0

代码

实际中，我们可以采用这样的代码，来显式让它先把 40 个处理了，再去把 960 处理。

对于最新的 RISC-V，可以用 setvl rd, rs1 指令来设置 vl = t0 = min(mvl, rs1)，从而简化代码逻辑。

Optimization¶

Vector Chaining¶

我们从 load unit 中取数据，是以串行+流水线的方式获取数据。

如图，由于三条指令之间存在 RAW 依赖关系，因此可以实现 chaining。

具体流程见下图：

Conveys and Chimes¶

我们在实际中，使用 conveys and chimes 技术来实现 vector chaining 这个概念。

概念

如图，图中一共有 2 个 RAW 依赖链：

指令 1、2
指令 3、4、5

由于 3 是 ld、5 是 sd，因此两者无法在一起执行，从而第二个链需要分成两个 chimes——总共需要 3 个 chimes。

对于足够长的 vector，最大的 overhead 就是串行加载/存储 vector register。一个 chime 里面只有一个这样的 overhead，因此三个 chimes 就是 3 个 overhead。

Chaining's role in ILP and DLP

如果两条指令没有结构冲突，且没有 RAW 冲突，那么它们本身就可以放在一起执行。而且是真并行。这个其实和 DLP 没有什么关系——即便没有 DLP，我们也可以同时运行多个部件。

Chaining 是为了将有 RAW 依赖关系（但是没有结构冲突）的相邻指令放在一起来执行。不过这个并行没有那么“真”，因为本质上还是数据流依次通过两个部件（并不是并行通过两个部件之类的），只是数据不用从寄存器中取出来、存进去再取出来、存进去，而只用取出来一次、存进去一次。这个其实是 exploit 了 DLP——我们省下来的时间，其实是数据流进出的时间，并不是指令执行的时间。

Conditional Execution¶

显然，如果一个操作执行与否，只能在 runtime 的时候进行判断，那么 vanilla vadd/sub/mult/... 是无法发挥其并行性的。

因此，我们就需要这种 conditional 的方式。类似于 numpy 的掩码：

mask = a != b
a[mask] -= b[mask]

Compress and Expand¶

在 numpy 中，上面代码实际的操作就是 compress + expand

稀疏矩阵¶

Info

其实本质上就是 gather/scatter 指令的实际使用

对于稀疏矩阵而言，会额外有一个辅助数组，用于储存所有非零的 index。

假设上面的 D 就是辅助数组

如果需要存回去的话，就要用到 scatter（gather 的逆操作）

Observation: numpy 里面的 array，可以用 mask 或者 gather 的方式来变换数组（而且两者语法一样，都是 array[mask_or_gather]），其实和这里的概念是对应的

Multiple Lanes¶

就是在一个 vector 内部，也进行并行运算。

Multi-lane 可以和 chaining 相结合，这样，不仅 overhead 数量减少（chaining），一个 overhead 造成的时间消耗也减少了（multi-lane）。

Two Views of Vectorization¶

Info

不管哪一种视角，向量都是一样的。但是编译器做优化的时候，trade-off 会不一样。

第一种视角：Inner loop vectorization

这个机器的一个向量有 m 个向量，每个向量有 n 个 elements。

第二种视角：outer loop vectorization

这个机器有 n 个虚拟机，每个处理器有 m 个 registers。也就是说，一共 m 个指令，每条指令更新一个标量寄存器，一共有 n 个虚拟机运行这个指令。

其实就是视作 multi-threading，一共有 n 个 threads

GPU¶

Overview¶

GPU 采用 Single Instruction Multiple Threads 的视角（这里是 data as thread）。不过这里的 thread，直接由 GPU 硬件进行管理，不受应用程序或者操作系统的控制。

GPU Memory Structure¶

GPU memory is shared by all Grids (vectorized loops).
Local memory is shared by all threads of SIMD instructions within a Thread Block (body of a vectorized loop).
Private memory is private to a single CUDA Thread.

TODO

Multiprocessors¶

若干种模型¶

Shared Memory
- NUMA
  - CC-NUMA
  - NC-NUMA
- COMA
- UMA
Message Passing
- Massive Parallel Processor
  - Cluster
  - Grid
- Cluster of Workstation

另外，如果所有处理器都能通过共享主存来互相传递消息，那么就是集中式；如果只能通过专用的 message passing，那么就是分布式的。

Shared Memory¶

NUMA vs UMA¶

一目了然，不言而喻。

对于 UMA 而言，其 bandwidth 瓶颈就在 interconnect 这里，导致难以 scale up
- 也就是，一旦 scale up 之后，bandwidth 和 latency 就需要 trade off 了
对于 NUMA 而言，访问别的存储器代价会大得多，因此编程或者编译的时候就会麻烦得多
- 也就是，假如说不关注每一块处理器使用的内存的话，那么 interconnect 又会成为瓶颈，而且此时延迟比 UMA 更大
- 当然，对于 NUMA 而言，无论怎样 scale up，如果每一个处理器主要都是使用其本身的内存，那么 latency 都是常数

Pros and Cons¶

好处很显然：

编程方便，可以视为只有一块内存
编程方便，指令只需要用 ld 和 sd

坏处：

处理数据的一致性会比较棘手
同时，数据保护也会成为一个问题
Scalability 也不太好，因为 communication model is so tightly coupled with process address space

Message Passing¶

我们现在越来越少用 message passing 了

每当需要无法直接使用 memory access 取到的数据的时候，就去进行 I/O 调用，“显式”地获取其它 processor 的数据。

Pros and Cons¶

好处：

Communication 是显式的、精确的
硬件简单（只需要整一个 I/O 接口就行）

坏处：

编程模型复杂

Trends¶

tl;dr: 共享内存，局部 UMA，全局 NUMA。

因此，我们着重需要解决 shared memory 的问题——synchronization

Cache Coherence¶

如果满足以上三点，那么我们就说这个 model 满足了 cache coherence。

不过，这样的要求还是不太现实：

不同处理器之间根本无法保持同步，两个处理器之间的先后顺序其实毫无意义
Cache 到 memory 的 propagation 需要时间，因此另外一个处理器完全有可能在还没有 propagate 完成前，就执行了 write 操作，因此第三条也是几乎不可能的

因此，我们把上面三条弱化成下面两条：

Any write must eventually be seen by a read
- 注意这里是 eventually，不是 immediately
All writes are seen in proper order
- 注意这里是 proper order（i.e. 任意 order，只要所有处理器都认为是这个 order），不是 time order

Snooping 协议¶

基本思想：一个处理器对某个内存地址完成了写操作之后，就需要将本次操作通过总线广播出去。然后，所有 cache 会根据总线上的信息，主动做一个响应。

分为两种协议：

Write Invalidate
- 在写的时候，总线上广播的数据只包含 address；其它处理器的 cache 接收到之后，如果 address 在 cache 中，就需要将其标为 invalid
- 在读的时候
  - 如果是 write through，就简单了，其它处理器在写 cache 的时候，已经将数据写进了 memory，因此直接读取 memory 就行
  - 如果是 write back，那么需要通过总线广播 address，让其它处理器的 cache 把对应的数据写进 memory 中，然后我再去 memory 把最新的数据读进来
Write Broadcast:
- 在写的时候，总线上广播的数据包含 address 和写入数据；其它处理器的 cache 接收到之后，如果 address 在 cache 中，可以直接将 cache 中对应的数据进行更改
- 在读的时候
  - 总线上广播的数据已经包含 address 和写入数据了，那么我们必然和 write through 搭配使用

上面的协议只保证了 writes must eventually be seen by a read。至于 seen in proper order，由于总线本身就是独占的，所有 processor 都会去抢总线资源，这个抢到的顺序，就自然决定了这个 "proper order"。

Example: Write Invalid + Write Back¶

如图，cache 一共会有三种状态。不过好消息是，这三种状态都可以用之前已经存在的 valid bit 和 dirty bit 来表示，因此无需增加新的 bit。

下面是状态转移表，以及转移时：

	Invalid	Shared	Exclusive
收到本地读请求	Shared (在总线上广播读请求)	-	-
收到本地写请求	Exclusive (在总线上广播读请求 + 写入 + 在总线上广播写通知)	Exclusive (在总线上广播写通知)	- (在总线上广播写通知)
收到远程读请求	-	- (反正与我无关)	Shared (写回内存)
收到远程写通知	-	Invalid	Invalid (写回内存)

注：按照这个协议，如果全局存在 exclusive，那么其它所有都必须是 invalid；如果全局不存在 exclusive，那么就是 invalid 或者 shared

More Protocols¶

MESI 协议¶

如图，增加了 exclusive 的状态：目前缓存和主存一样，而且和其它处理器的不同（说白了就是其它处理器都是 invalid——还没有读这一块数据）

状态转移如下：

注意：read-for-ownership 会将其它所有处理器设为 invalid.

好处：处在 exclusive 状态下，CPU write 的时候，不需要在总线上广播 write；CPU read 的时候，不需要在总线上广播 read。如果我们确实需要读入一个数据，然后做很多操作，那么这样做可以大大减小延迟和负载。

Performance¶

如上，

true sharing miss 就是因为其它处理器写，然后我读的时候就会 miss
false sharing miss 是因为 MESI 协议会直接将所有其它处理器对应地址的 cache 标为 invalid，如果该处理器对这个地址的数据没有做任何修改的话，那么就相当于平白无故将其它 cache 标为 invalid

实际测试发现：True sharing miss 占比本身不小，且不显著随着 cache 增大而减小，因此使我们优化的重点；而 false sharing miss 基本可以忽略。

内存一致性¶

Coherence vs Consistency

Coherence 的两个要求：

All write must be eventually seen
Writes must been seen in the same order by all processors

e.g. 消息对方必须收到、所有人收到的次序必须一样。

Consistency 是针对所有 addresses 的：writes must been seen in a certain order by all processors

e.g. （以 SC 模型为例）所有人收到的次序，必须和每个人发送的次序不冲突。

内存一致性考虑的是多个处理器访问同一块共享内存的行为。和之前的缓存一致性不同，内存是处理器之间共享的。

有四个比较经典的模型：

顺序一致模型（sequential consistency model，SC）
完全存储定序（total store order，TSO）
部分存储定序（part store order，PSO）
宽松存储模型（relax memory order，RMO）

SC：顺序一致性¶

顺序一致性是最简单的内存模型，也称为强定序模型。CPU会按照程序顺序来执行所有的load与store动作，即按照它们在程序中出现的次序来执行。从主存储器和CPU的角度来看，load和store是顺序地对主存储器进行访问。PS：可以想象成只有共享存储，没有独立存储。

顺序一致性内存模型是一个被计算机科学家理想化了的理论参考模型，它为程序员提供了极强的内存可见性保证。顺序一致性内存模型有两大特性：

一个线程中的所有操作必须按照程序的顺序来执行。
（不管程序是否同步）所有线程都只能看到一个单一的操作执行顺序。

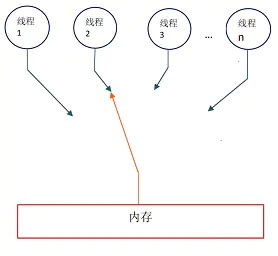
在顺序一致性内存模型中，每个操作都必须原子执行且立刻对所有线程可见。顺序一致性内存模型为程序员提供的视图如下：

在概念上，顺序一致性模型有一个单一的全局内存，这个内存通过一个左右摆动的开关可以连接到任意一个线程，同时每一个线程必须按照程序的顺序来执行内存读/写操作
从上面的示意图我们可以看出，在任意时间点最多只能有一个线程可以连接到内存。当多个线程并发执行时，图中的开关装置能把所有线程的所有内存读/写操作串行化（即在顺序一致性模型中，所有操作之间具有全序关系）。

为了更好的理解，下面我们通过一个示意图来对顺序一致性模型的特性做进一步的说明。

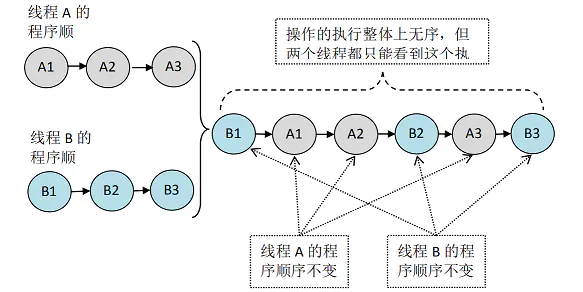
假设有两个线程 A 和 B 并发执行。其中 A 线程有三个操作，它们在程序中的顺序是：A1->A2->A3。B 线程也有三个操作，它们在程序中的顺序是：B1->B2- >B3。

未同步程序在顺序一致性模型中虽然整体执行顺序是无序的，但所有线程都只能看到一个一致的整体执行顺序。以上图为例，线程 A 和 B 看到的执行顺序都是：B1- >A1->A2->B2->A3->B3。之所以能得到这个保证是因为顺序一致性内存模型中的每个操作必须立即对任意线程可见。

TSO：完全存储定序¶

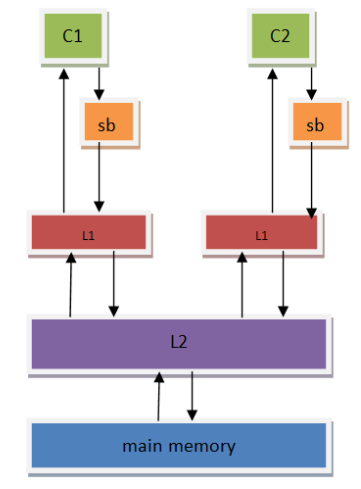
为了提高CPU的性能，芯片设计人员在CPU中包含了一个存储缓存区（store buffer），它的作用是为store指令提供缓冲，使得CPU不用等待存储器的响应。所以对于写而言，只要store buffer里还有空间，写就只需要1个时钟周期（哪怕是ARM-A76的L1 cache，访问一次也需要3个cycles，所以store buffer的存在可以很好的减少写开销），但这也引入了一个访问乱序的问题。

相比于以前的内存模型而言，store的时候数据会先被放到store buffer里面，然后再被写到L1 cache里。

首先我们思考单核上的3条指令：


1 2 3	复制 S1：store flag= set S2：load r1=data S3：store b=set

如果在顺序存储模型中，S1肯定会比S2先执行。但是如果在加入了store buffer之后，S1将指令放到了store buffer后会立刻返回，这个时候会立刻执行S2。S2是read指令，CPU必须等到数据读取到r1后才会继续执行。这样很可能S1的store flag=set指令还在store buffer上，而S2的load指令可能已经执行完（特别是data在cache上存在，而flag没在cache中的时候。这个时候CPU往往会先执行S2，这样可以减少等待时间）

这里就可以看出再加入了store buffer之后，内存一致性模型就发生了改变。引入了store-load乱序。

如果我们定义store buffer必须严格按照FIFO的次序将数据发送到主存（所谓的FIFO表示先进入store buffer的指令数据必须先于后面的指令数据写到存储器中），这样S3必须要在S1之后执行，CPU能够保证store指令的存储顺序，这种内存模型就叫做完全存储定序（TSO）。

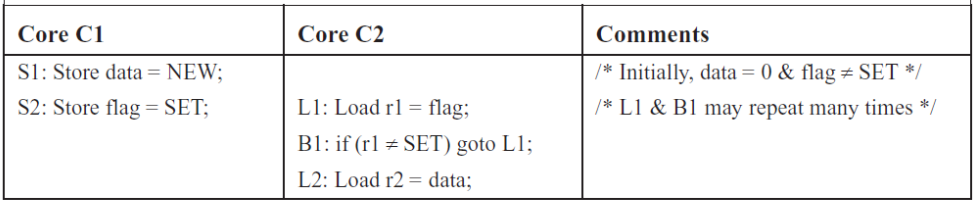
经典的例子：

在SC模型里，C1与C2是严格按照顺序执行的，代码可能的执行顺序如下：


1 2 3 4 5 6	S1 S2 L1 L2 S1 L1 S2 L2 S1 L1 L2 S2 L1 L2 S1 S2 L1 S1 S2 L2 L1 S1 L2 S2

由于SC会严格按照顺序进行，最终我们看到的结果是至少有一个CORE的r1值为NEW，或者都为NEW。

在TSO模型里，由于store buffer的存在，L1和S1的store指令会被先放到store buffer里面，然后CPU会继续执行后面的load指令。Store buffer中的数据可能还没有来得及往存储器中写，这个时候我们可能看到C1和C2的r1都为0的情况。

所以，我们可以看到，在store buffer被引入之后，内存一致性模型已经发生了变化（从SC模型变为了TSO模型），会出现store-load乱序的情况，这就造成了代码执行逻辑与我们预先设想不相同的情况。而且随着内存一致性模型越宽松（通过允许更多形式的乱序读写访问），这种情况会越剧烈，会给多线程编程带来很大的挑战。

PSO：部分存储定序¶

芯片设计人员并不满足TSO带来的性能提升，于是他们在TSO模型的基础上继续放宽内存访问限制，允许CPU以非FIFO来处理store buffer缓冲区中的指令。CPU只保证地址相关指令在store buffer中才会以FIFO的形式进行处理，而其他的则可以乱序处理，所以这被称为部分存储定序（PSO）。

S1与S2是地址无关的store指令，cpu执行的时候都会将其推到store buffer中。如果这个时候flag在C1的cahe中不存在，那么CPU会优先将S2的store执行完，然后等flag缓存到C1的cache之后，再执行store data=NEW指令。

这个时候可能的执行顺序：


1	复制 S2 L1 L2 S1

这样在C1将data设置为NEW之前，C2已经执行完，r2最终的结果会为0，而不是我们期望的NEW，这样PSO带来的store-store乱序将会对我们的代码逻辑造成致命影响。

从这里可以看到，store-store乱序的时候就会将我们的多线程代码完全击溃。所以在PSO内存模型的架构上编程的时候，要特别注意这些问题。

RMO：宽松内存模型¶

丧心病狂的芯片研发人员为了榨取更多的性能，在PSO模型基础上，更进一步的放宽了内存一致性模型，不仅允许store-load，store-store乱序。还进一步允许load-load，load-store乱序，只要是地址无关的指令，在读写访问的时候都可以打乱所有load/store的顺序，这就是宽松内存模型（RMO）。

实际上，RMO 也细分两种：Weak Ordering 以及 Release Consistency。两者的差别在于 synchronization，也就是

WO 保证了所有读写操作，和 synchronization 指令的顺序不变（i.e. 保证 \(R/W \to S, S \to R/W, S \to S\)）
RC 将 S 细分为 Sync Acquire 和 Sync Release，两者分别只保证 \(S_A \to R/W, R/W \to S_R, S_{A/R} \to S_{A/R}\)
- 无法保证 \(R/W \to S_A, S_R \to R/W\)
- 不过，如果使用一对 \(S_RS_A\)，那么就和 WO 中的 \(S\) 等价
- RC 相当于 WO 的细化版