Alpha-Beta 剪枝详解

节点需要记录的数据

每一个节点，只需要记录：

• 自己的类型：min | max
• 子节点
  • 也许可以实时动态算出来，就无需记录了
• alpha: int | -∞
  • i.e. 下界
• beta: int | +∞
  • i.e. 上界
• value: int | null

节点初始化

所有节点的 alpha 和 beta 都是 -∞, +∞。

叶子节点的 value 就是对应的 value（赢、输），非叶子节点的 value 就是 null。

信息传递方法

向下传递：

将 alpha, beta 传给 child。

子节点将传递来的 alpha, beta 值，当成自己的 alpha, beta（从而代替 ±∞）

• 这个意思就是：假如这个子节点可以取到自己的目标值，那么，就必须满足的 alpha beta 条件

向上传递：

将 value 传给 parent。

parent 根据自己的类型，决定更新 alpha(max) 或者 beta(min)。

搜索方法

如果自己是叶子节点，就

• 直接返回 value。

如果自己不是叶子节点，就

1. 逐一递归子节点
   • 同时传递 alpha 和 beta
2. 将子节点的 value 赋予自己的 alpha(max) 或者 beta(min)
3. 将子节点的 value 和自己当前的 value 进行比较，更新自己的 value
4. 如果出现了 beta ≤ alpha 的情况，就剪枝
   • 也就是：停止搜索，直接返回当前的 value
   • 因为，既然已经 β ≤ α 了，
     • 要不然就是 β=α——即使这个节点可以取到 parent node 的目标值，也不可能改变 the value of parent node
     • 要不然就是 β<α——这个节点已经不可能取到自己的目标值了，game over
5. 如果搜索完了所有子节点，就返回
6. 如果上述两者都不满足，那就重复 (1)

例子

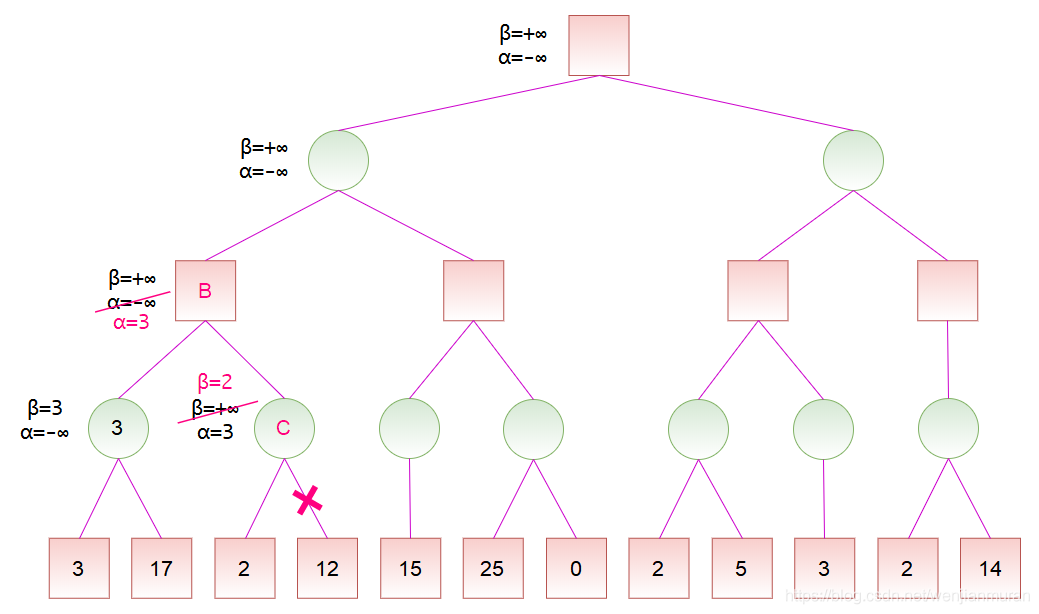
如上图所示：

1. B 搜索左节点之后，左节点返回 3
2. B 是 max 节点，因此更新 α: α=3
3. B 传给 C: \(\alpha_C = 3, \beta_C = +\infty\)
4. C 搜索左节点
5. 由于 C 的左节点是叶子节点，因此直接返回 value
6. C 是 min 节点，因此更新 β: β=2
7. 由于出现了 β=2 ≤ alpha=3 的情况，因此剪枝，不管右节点（i.e. 12）了，直接返回值：2
8. ……