2. Arithmetics
加法器¶
Carry Select Adder¶
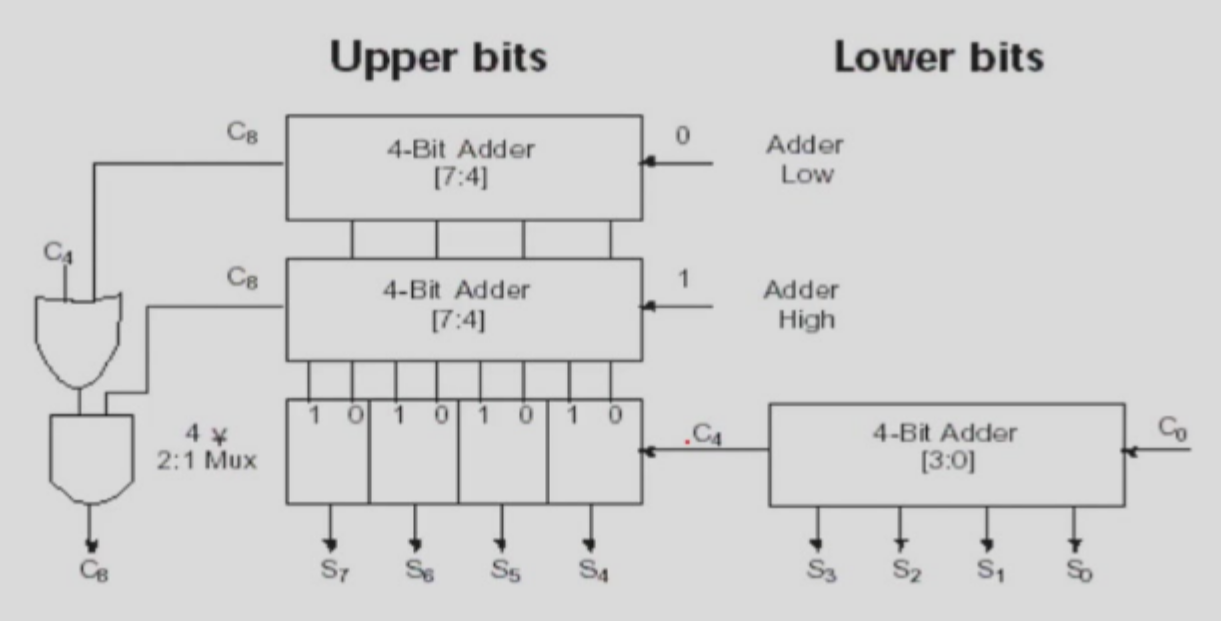
本质上,如果要算加法,只需要前面的进位就可以算。那么,我们就可以
- 超前进位,让进位更快地算出来
- 猜测进位(如上图),直接算两个结果出来,然后根据最后实际的进位来选择
本例中,我们使用了 carry select adder,将二进制数分成若干块,块与块之间的加法可以并行计算,算完之后只需要通过上一个进位来选择即可。
本质上,这就是空间换时间。
乘法器¶
无符号乘法器¶
注:我们以 64 位乘法为例。
Naive Multiplier V1¶
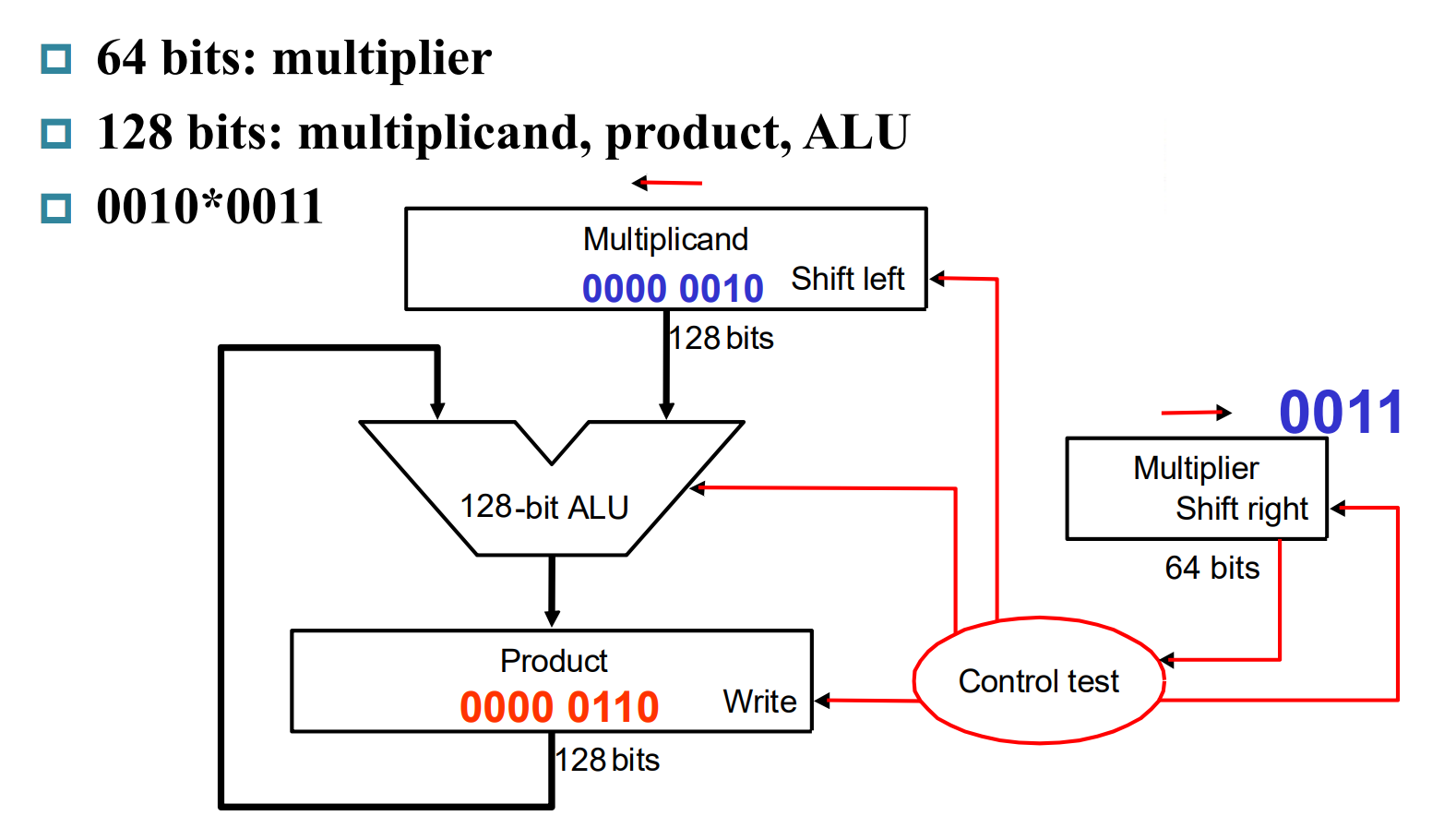
如图,由于我们需要对 multiplicand 进行移位(类比:我们列竖式不就要移位嘛),因此需要 128 位储存 multiplicand 和 product,同时还需要 128 位 ALU。
Naive Multiplier V2¶
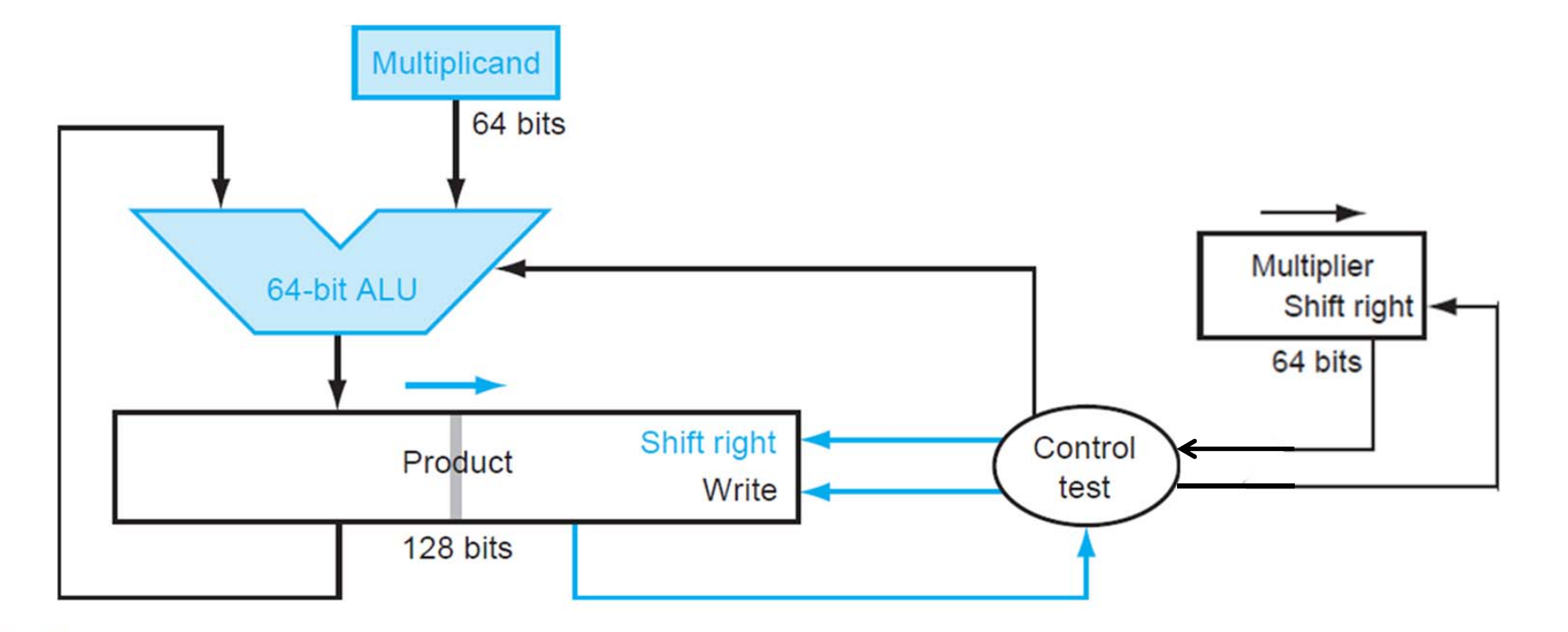
如图,我们做了一个小优化:移位是相对的。与其移位 multiplicand,不如移位 product。这样,我们就只需要 64 位 multiplicand 了。更关键地,我们只需要 64 位 ALU 了,速度提升至少一倍。
Naive Multiplier V3¶
进一步,我们发现,右上的 multiplier shift right 和 中间的 product shift right 是同步进行的。
因此,我们不妨直接把 multiplier 放到 product 右边 64 bits 那里,然后每一次只需要进行一次移位(product)即可,从而进一步节省空间和加速。(如下图,不过注意下图是 32 位,不是 64 位的)
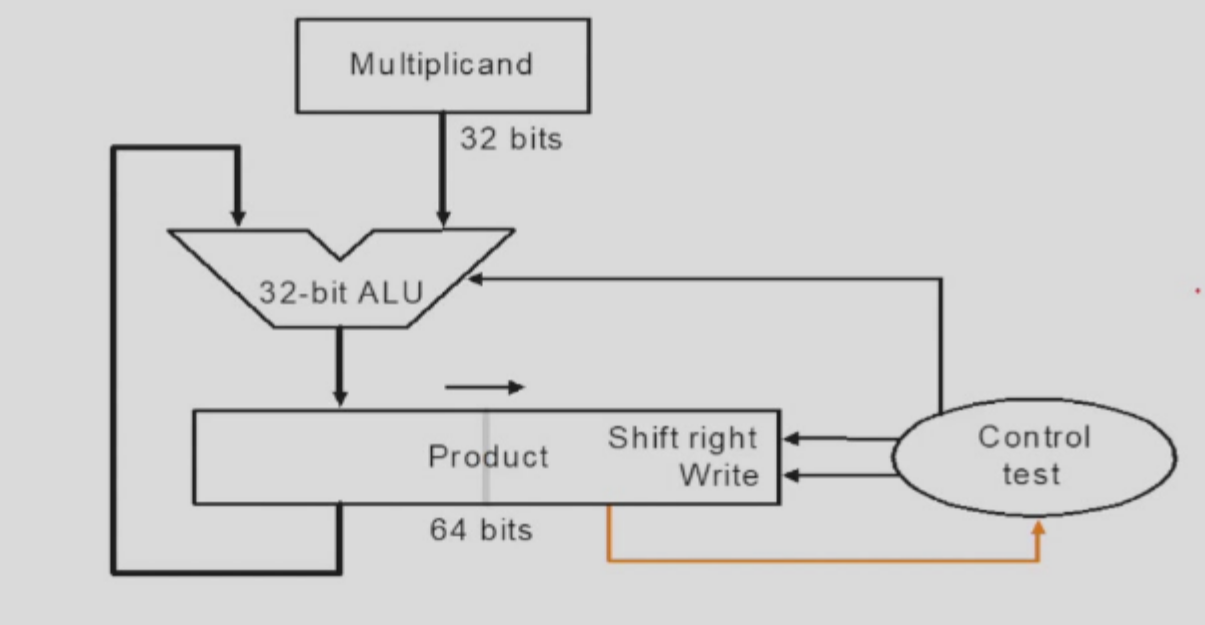
Naive Multiplier V3 的流程如下:
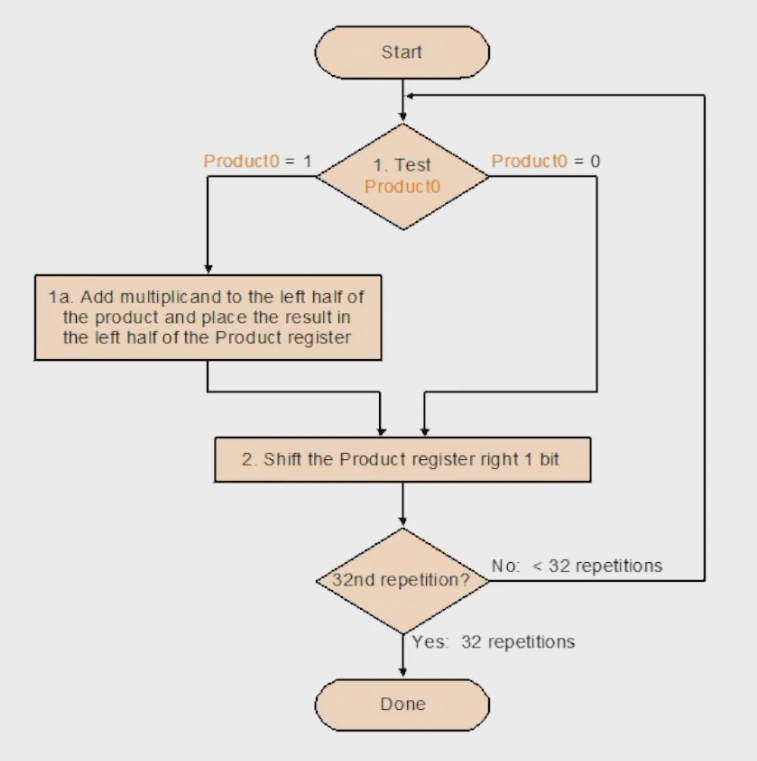
有符号乘法器¶
有符号的数字,如果相乘之后扩展其位数(比如,我们对两个 32 位整数进行相乘,然后将结果储存在 64 位整数中),那么,就不可以直接相乘。
- 比如:对于 8-bit * 8-bit -> 16-bit,
11111111 * 11111111 = 1111111000000001 != 0000000000000001
一个 naive 的想法就是
- 先对其符号进行相乘
- 两数转变成绝对值再相乘
- 最后根据原符号来确定最后的值的正负
不过这样做并不方便,而且比较慢。
Booth 算法¶
对于 multiplier,我们以前只关注目前的位(记为 \(\newcommand{vc}{v_{cur}}\vc\))
- 如果 \(\vc=1\),那么加上 multiplicand
- 如果 \(\vc=0\),那么就不做加法
现在,我们关注目前的位以及之前的位(记作 \(\newcommand{vp}{v_{prev}}\vp\))。并且,规则也有所变化(见下表)
| \((\vc, \vp)\) | operation |
|---|---|
| \((0,0)\) | No operation |
| \((0,1)\) | Add multiplicand |
| \((1,0)\) | Substract multiplicand |
| \((1,1)\) | No operation |
- 注意:最开始的时候,由于 \(\vc\) 之前并没有值,我们约定 \(\vp\) 最初为 0。
例子¶

如图:
- 由于 booth 算法需要记录 \(\vc, \vp\)(见上图红圈内),因此 product 需要再添加一位,用于记录 \(\vp\)
- 另外可见 \(\vp\) 最初恒为 0
- 移位的时候,不要改变符号位
1110 0010->1111 0001,0110 0010->0011 0001
- 最后,乘数和被乘数是多少位的乘法,就进行多少个 iteration
快速乘法¶
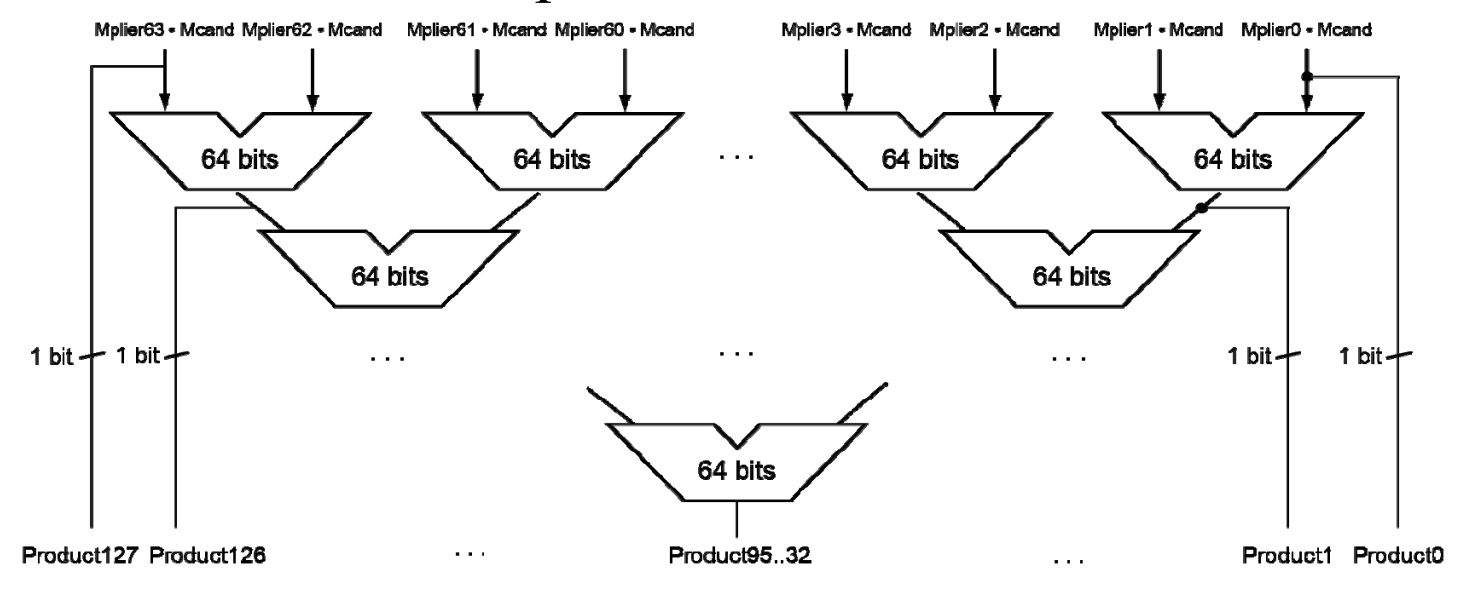
如图,64 位数乘 64 位数,相当于 64 位 64 位数相加。
除法器¶
Dividend (被除数) ÷ Divisor (除数)
- 将除数放到高位。从高位开始减,减完将除数右移。商也随之不断左移。如果减完之后是负数,需要还回去。
Naive iteration¶
- 将 quotient 左移一位
- remainder 减去 divisor
- 判断 remainder 的大小
- 如果小于 0,那么加回去,其它什么也不做
- 如果大于等于 0,那么就不加回去,并且将 quotient 的最后一位由 0 变成 1
- 将 divisor 右移一位
例子:7 ÷ 2¶
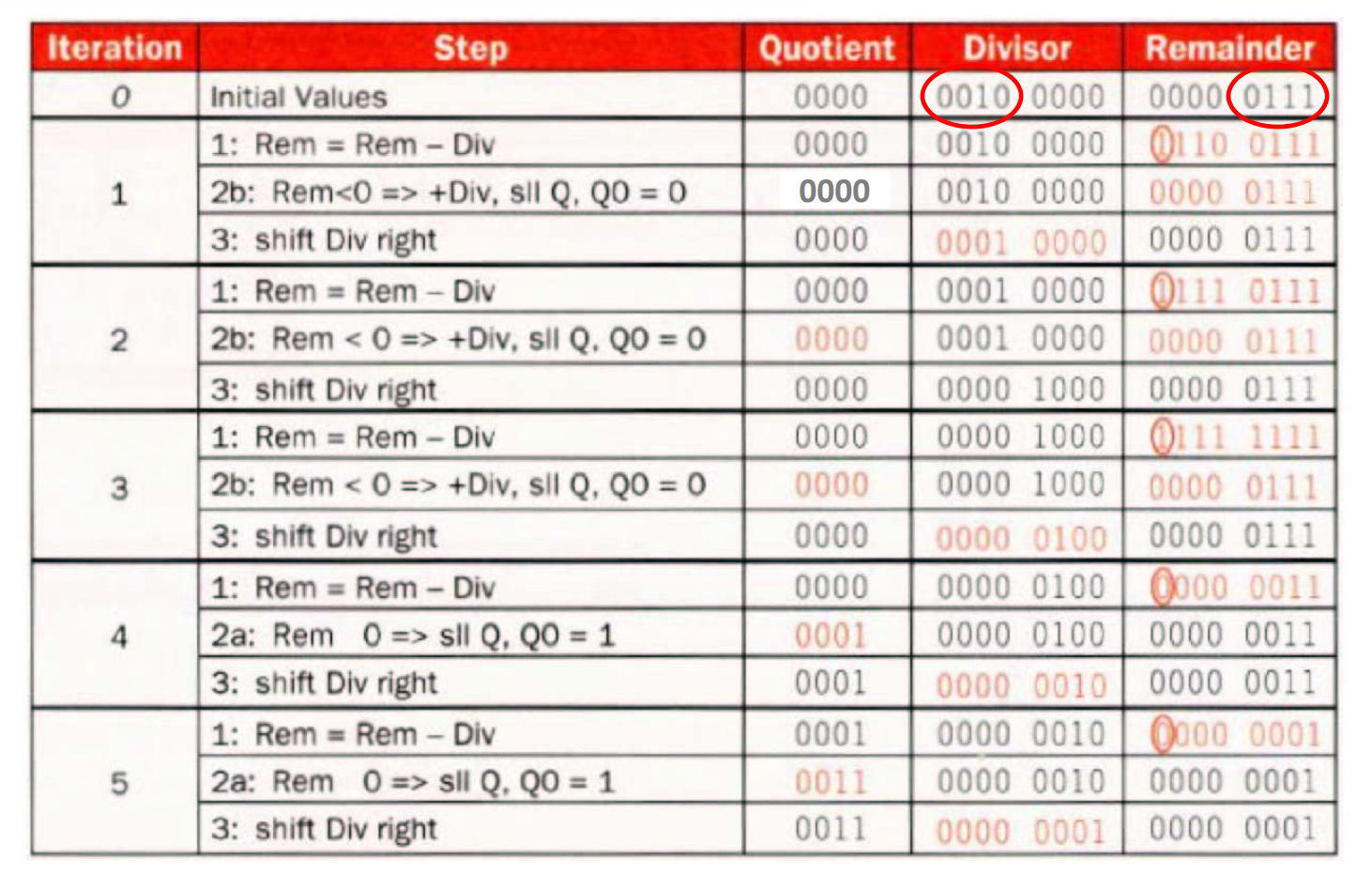
| 将 quotient 左移一位 | remainder 减去 divisor | 判断 remainder 的大小 | 将 divisor 右移一位 |
|---|---|---|---|
| q0000 -> q0000 | r0000 0111 -> r1110 0111 | <0, r1110 0111 -> r0000 0111 | d0010 0000 -> d0001 0000 |
| q0000 -> q0000 | r0000 0111 -> r1111 0111 | <0, r1111 0111 -> r0000 0111 | d0001 0000 -> d0000 1000 |
| q0000 -> q0000 | r0000 0111 -> r1111 1111 | <0, r1111 1111 -> r0000 0111 | d0000 1000 -> d0000 0100 |
| q0000 -> q0000 | r0000 0111 -> r0000 0011 | ≥0, q0000 -> q0001 | d0000 0100 -> d0000 0010 |
| q0001 -> q0010 | r0000 0011 -> r0000 0001 | ≥0, q0010 -> q0011 | d0000 0010 -> d0000 0001 |
如图,被除数是 b0111,除数是 b0010。除数和被除数如果长度为 n,就要进行 (n+1) 次 iteration
Better iteration¶
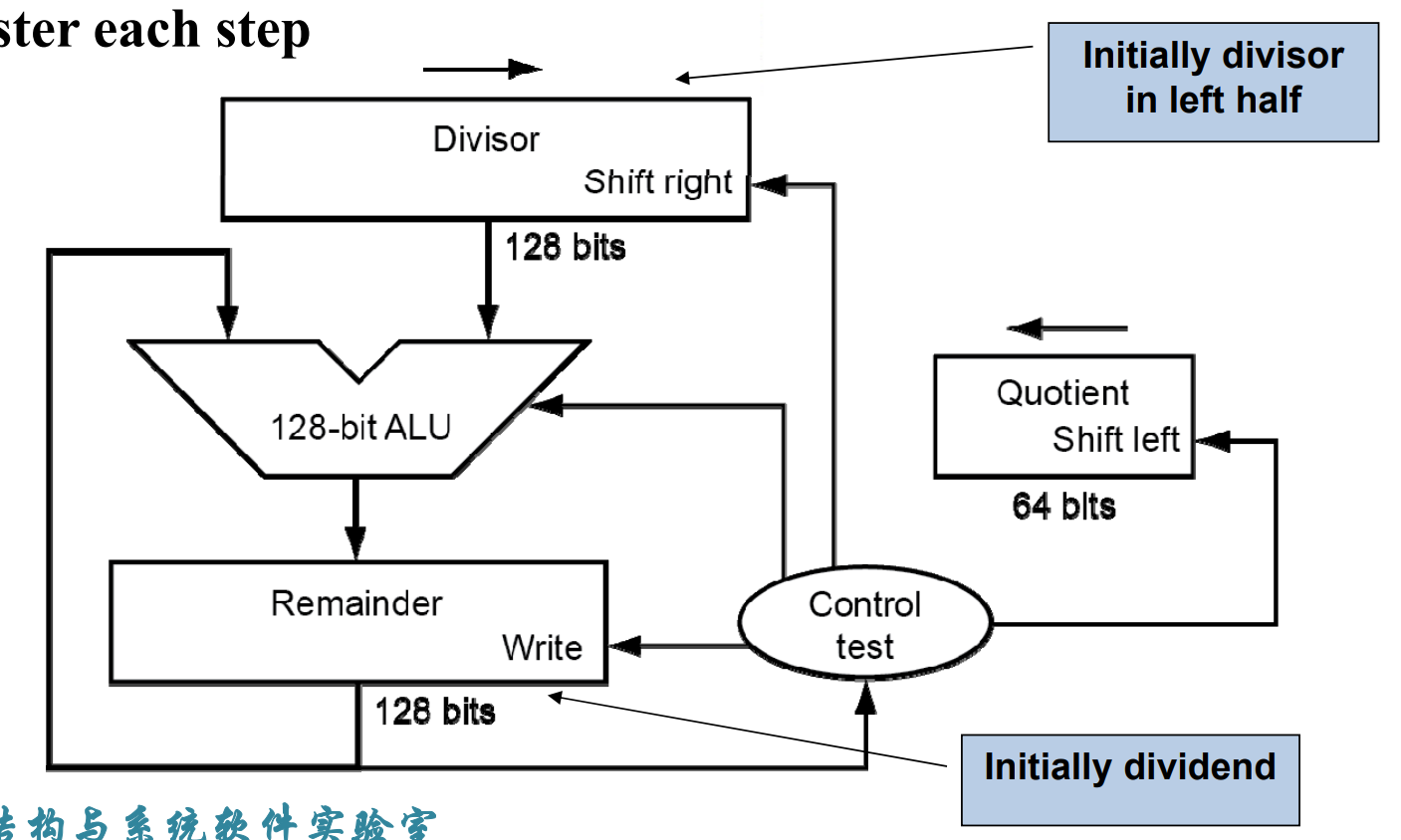
实际的 ALU中,我们采用的是将被除数左移、商放到被除数右侧的方式。
- 左移 remainder(否则第一步必然小于 0,就浪费了)
- remainder 减去 divisor
- 判断 remainder 的大小
- 如果小于 0,那么
- 加回去,然后左移 remainder
- 如果大于等于 0,那么就
- 不加回去,直接左移 remainder
- 然后将 remainder 的最后一位由 0 变成 1
- 如果小于 0,那么
- 重复第 2 步,重复的次数就是 divisor 的长度
- 右移 remainder 左半部分(抵消第 1 步)
例:7 ÷ 2¶
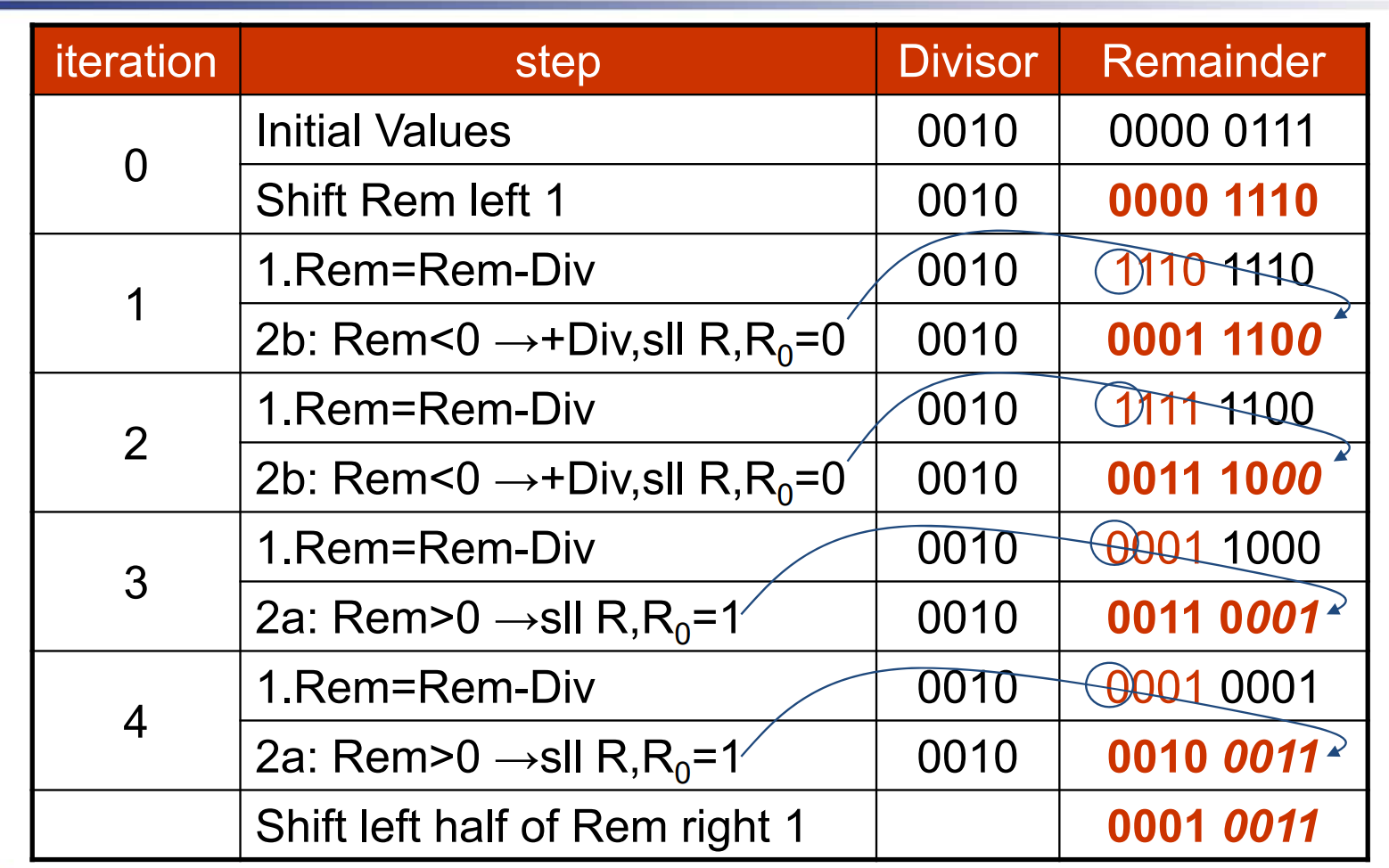
例:7 ÷ 0(非法操作)¶
左移 remainder: r0000 0111 -> r0000 1110
| remainder 减去 divisor | 判断 remainder 的大小 |
|---|---|
| r0000 1110 -> r0000 1110 | ≥0: r0000 1110 -> r0001 1101 |
| r0001 1101 -> r0001 1101 | ≥0: r0001 1101 -> r0011 1011 |
| r0011 1011 -> r0011 1011 | r0011 1011 -> r0111 0111 |
| r0111 0111 -> r0111 0111 | r0111 0111 -> r1110 1111 |
右移 remainder 的高位: r1110 1111 -> r0111 1111
从而余数就是 7,商就是 1111。
更复杂的除法¶
对于有符号除法,我们要求余数和被除数的符号相同。
IEEE 浮点数¶

| 形式 | 指数 | 小数部分 |
|---|---|---|
| 零 | 0 | 0 |
| 非规约形式 | 0 | 大于0小于1 |
| 规约形式 | 1 到 2e-2 | 大于等于1小于2 |
| 无穷 | 2e-1 | 0 |
| NaN | 2e-1 | 非0 |
单精度浮点数¶

单精度浮点数的值如下(不考虑符号)
IF (exp == 0)
THEN:
IF (frac == 0)
THEN:
0
ELSE:
0.frac * 2^{-126}
ELIF (isAllOne(exp))
THEN:
IF (frac == 0)
THEN:
Inf
ELSE:
NaN
ELSE:
1.frac * 2^{exp-127}
浮点数的间距是这样的:
- 最初的浮点数,从全 0 开始,你每加 1,它就加 $2^{-127+23}:=2^{-126 - 23}:=2^{-149} $
- 加了 \(2^{23}\) 次,就变成了规约形式,但是间距还不变
- 后来,在规约形式下,每加 \(2^{23}\) 次,间距就会翻倍
- 由于一共有 \(2^{31}\) 位,因此间距可以翻倍 \(2^{31 - 23} - 3 := 253\) 次,也就是间距从原来的 \(2^{-149}\) 最多变成的 \(2^{104}\)
- 也就是说,单精度浮点数可以表示的最大实数就是 \(2^{127 + 1} - 2^{104}\)
下图是一个直观的认知(注意绿色段和右侧相邻的等长的黑色段的间距是一样的):
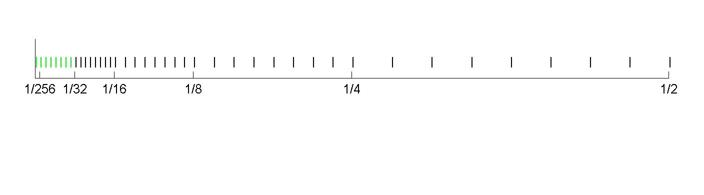
四则运算¶
浮点数的四则运算,本质上就是整数的四则运算(可能还要进行移位等操作),只不过指数部分需要额外处理,另外也需要处理符号位。
乘法¶

如图,乘法只需要
- exponents 相加
- 两数相乘
- normalize(避免 overflow/underflow)
- round 一下
- 确定 sign 的正负
记录一下(与上文无关)¶
一个 object file 的
- 符号表:符号+符号对应的位置
- 重定位信息:
- RISC-V:重定位数据的所在指令的起始位置+命令类型+对应符号
- 因为 RISC-V 的指令很少,而且每条指令至多一个需要重定位的数据,因此可以这样做
- x86:重定位数据的起始位置+数据长度+对应符号(的 index)
- RISC-V:重定位数据的所在指令的起始位置+命令类型+对应符号
GCC 进行多文件编译的时候,可以在逻辑上理解成:
- 逐个扫描每个 obj 的重定位信息,添加到其 undefined symbol table
- 同时,逐个扫描每个 obj 和 library 的符号表,
- 如果是 obj,那么对于当前文件所有的符号
- 如果是强符号,且 symbol table 里这个符号为强符号,就报错
- 如果是强符号,且 symbol table 里这个符号不是强符号(或没有),就将其加入 symbol table,记作弱符号,同时记录地址
- 如果是弱符号,且 symbol table 里这个符号为强符号或者弱符号,就直接忽略
- 如果是弱符号,且 symbol table 里这个符号没有,就将其加入 symbol table,记作弱符号,同时记录地址
- 如果是 library,操作类似。但是由于库的符号实在太多,因此我们一般只会考虑将目前已经在 undefined symbol table 里的符号加入 symbol table。
- 如果是 obj,那么对于当前文件所有的符号
- 在记录了所有符号的重定位位置之后,再进行二次扫描,并且给每一个符号进行重定位
因此,由于所有 obj 的符号都会包含,因此不用关心顺序;由于 library 只会包含目前已经在 undefined symbol table 的符号,因此需要考虑顺序。
注意¶
实际上,GCC 比这复杂的多。
比如,
然后将 1.c 和 2.c 编译成静态库 lib1.a, lib2.a。
如果是
// main.c
##include <stdio.h>
int food()
{
return 114514;
}
int x;
int main()
{
// printf("%d\n", food());
return 0;
}
那么
就无法通过。显示错误
/usr/bin/ld: ./lib1.a(1.o): in function `food':
1.c:(.text+0x0): multiple definition of `food'; /tmp/ccGkQvtL.o:3.c:(.text+0x0): first defined here
collect2: error: ld returned 1 exit status
但是,如果是
// main.c
##include <stdio.h>
int food()
{
return 114514;
}
int x = 114514;
int main()
{
// printf("%d\n", food());
return 0;
}
或者
就可以通过。