Lec 2: Equations¶
Bisection¶
注意两点:
可用于任意连续函数
Fix-point Method¶
我们希望把方程 \(f(x) = 0\) 转换成 \(x = g(x)\)。
- 比如:\(x^2 - 5x +1= 0\) 转换成 \(g(x) = f(x) + x = x^2 -4x + 1=x\)
我们从 \(p_0\) 开始,按照上述递推关系,求出一个序列 \(\{p_i\}_{i \in \mathbb{N}}\),使得:\(p_{i+1} = g(p_i)\)
如果 \(\lim_{i \to \infty} p_i = p^*\),且 \(g\) 连续,那么:
Fix-point Theorem¶
Theorem 1: 假如
- \(g \in C[a,b]\) s.t. \(g(x) \in [a,b]\)
- 保证值域包含于定义域内
- \(\exists k \in (0,1), \forall x \in (a,b): \lvert g'(x) \rvert \leq k\)
- \(p_0 \in [a,b]\)
- 保证数学归纳法的 initial condition is satisfied
那么,上述数列一定收敛
Proof: $$ \frac {\lvert p_{i+2} - p_{i+1} \rvert} {\lvert p_{i+1} - p_{i} \rvert} = \frac {\lvert g(p_{i+1}) - g(p_{i}) \rvert} {\lvert p_{i+1} - p_{i} \rvert} = \lvert g'(\xi) \rvert \leq k $$ 通过数学归纳法,可以容易证明 \(g(p_0) \neq p_0 \implies \{p_i\}_{i \in \mathbb{Z}^+} \in (a,b)\) ,从而就在我们讨论的定义域内。
- 如果 \(g(p_0) = p_0\),就没有算的必要了
由于两项之差以至少指数级的速度收敛(以及每一项与真值之差),因此是 Cauchy 列,容易证明收敛。
Corollary 1: $$ | p _ { n } - p | \leq \frac { 1 } { 1 - k } | p _ { n + 1 } - p _ { n } | \text{ and } | p _ { n } - p | \leq \frac { k ^ { n } } { 1 - k } | p _ { 1 } - p _ { 0 } | $$ Proof: 易证
根据推论,我们可以
- 通过 \(| p_1 - p_0 |\) 来确定最多迭代次数
- 通过 \(| p _ { n+1 } - p _{n}|\) 来实时判断停止
Newton's Method¶
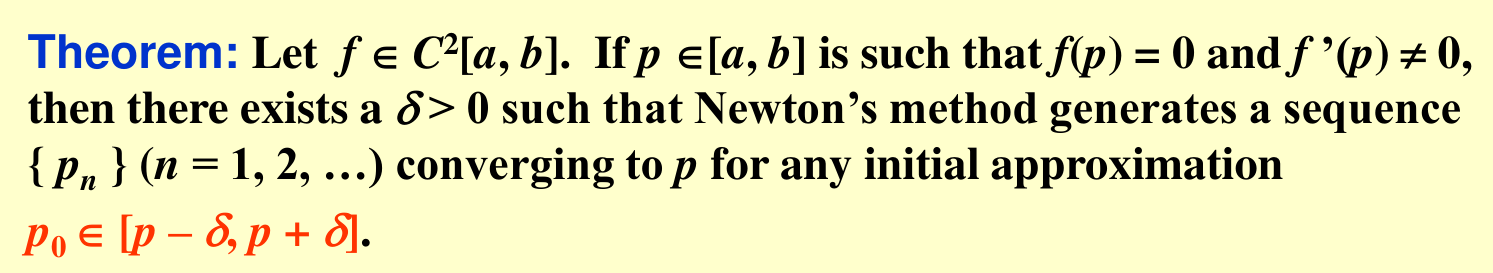
Proof:
令 \(g(x) = x - \frac {f(x)}{f'(x)}\),然后我们可以去套 fix-point method 的条件。
First condition: \(g \in C[p - \delta, p + \delta]\) s.t. \(g(x) \in [p - \delta, p + \delta]\)
\(|g(x) - p| = |g(x) - g(p)| = |x-p||g'(\xi)| \leq k|x-p| \leq |x-p| \leq \delta\)
- 需要依靠 second condition 的保证
- 另外,在 Newton's Method 下,second condition(以及 \(g\) 可导)可以直接推出 first condition
- 因为,\(a=p-\delta, b=p+\delta\) 是关于 \(p\) 对称的
- 而一般的不动点定理的条件,并没有这样的条件
Second condition: \(\exists k \in (0,1), \forall x \in (p - \delta, p + \delta): \lvert g'(x) \rvert \leq k\)
\(g'(x) = \frac{f(x)f''(x)}{f'(x)^2}\),由于二阶导连续,一阶导不等于 0,因此 \(g'(x)\) 连续。
由于 \(f(p) = 0\),因此 \(g'(p) = 0\),因此,\(\forall k \in (0,1), \exists \delta > 0, \forall x \in [p - \delta, p + \delta]: |g'(x)| \leq k\)
Third condition: \(p_0 \in [p - \delta, p + \delta]\)
显然。
至于为什么 \(\delta\) 无法精确得到,这是因为我们并不知道 \(g'(x)\) 能够在那个范围内 bound 住。
如果能够推导出 \(g'(x)\) 能够在某个区域中,被某个 \(k \in (0,1)\) bound 住。那么,就能够更加保险地使用这个方法。
多项式求根¶
多项式求根的精确+高效算法,到现在还是一个 open problem。