Lec 0: Fundamentals of TDA¶
Simplex & Complex¶
简单来说,\(n\) 维单纯形,就是
- \(n+1\) 个点构成的点集所唯一描述的一个形状
- 区分:该形状是一个无穷点集,嵌入在 \(n\) 维空间。
不难发现,由于 \(\binom {n+1} {n} = n+1\),因此 \(n\) 维单纯形有 \(n+1\) 个面。
\(n\) 维单纯复形就是 \(0 \sim n\) 维单纯形的一个集合(记为 \(\K\)),并满足:
- \(\forall \sigma \in \K: \dim(\sigma) \geq 0 \implies \operatorname*{faces}(\sigma) \in \K\)
- 因为 \(0\) 维单纯形就是面
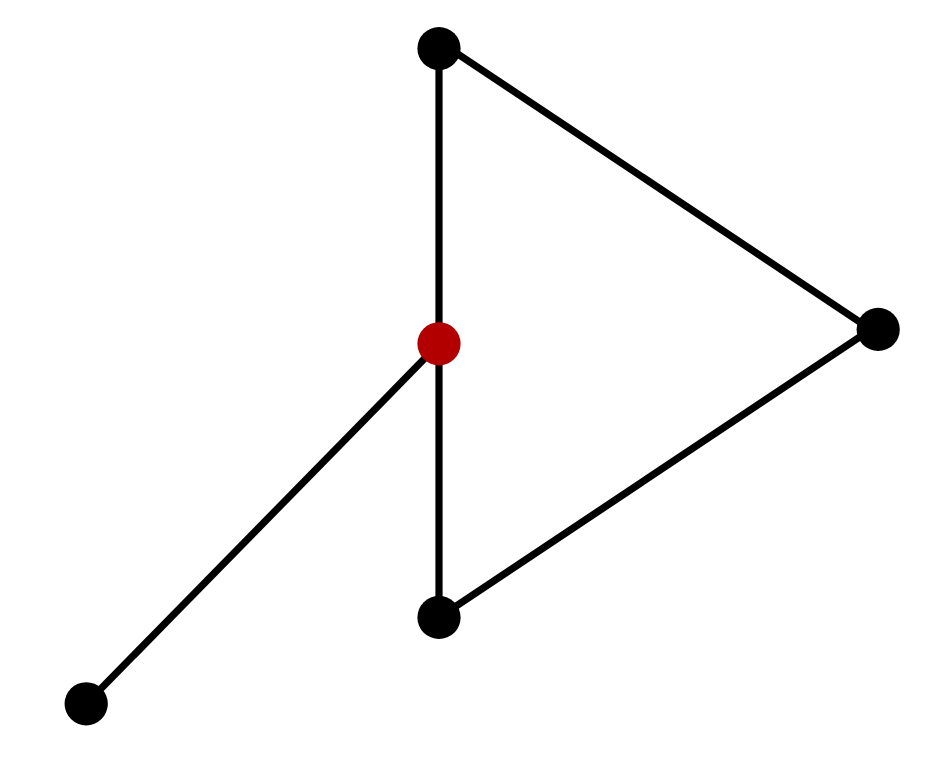
- \(\forall \sigma_1, \sigma_2 \in \K: \sigma_1 \cap \sigma_2 = \emptyset \text{ or } \sigma_{1,2},s.t. ~\sigma_3 \in \K\)
- 避免比如一条边和另一条边的端点相交(如图中红点)
- 注意:这两条边的描述点集没有交点,但是形状点集有交点
链群和边界算子¶
\(n\)-chain 是某单纯复形的 \(n\) 维单纯形集合。
我们可以为 \(n\)-chain 配备一个 Abelian 群,使得该 \(n\)-chain “扩展”成一个集合。称为 \(n\)-chain group (链群)
- 注意区分链和链群,后者是一个 Abelian 群,前者不是
我们往往会使用 \(\Z_2\) 群。
边界算子: $$ \partial(X) := \partial([v_0, v_1, v_2, \dots, v_n]) = \sum_{i=0}^n (-1)^i [v_0, v_1, \dots, \widehat{v_i}, \dots, v_n], \newline s.t. \widehat{v_i} \text{ means that } v_i \text{ is removed from this (oriented) simplex.} $$ e.g. $$ \partial([a,b,c]) = (-1)^0[b,c]+(-1)^1 [a,c] +(-1)^2 [a,b] = [b,c] - [a,b] + [b,c] = [b,c] + [a,c] + [a,b] $$
- 因为配备的群是 \(\Z_2\),所以 \(-[a,b] = [a,b]\)。
链复形¶
假设 \(S\) 是单纯 \(p\) 复形,那么,链复形 \(\mathscr C(S) = \sum_{n=0}^p \partial(C_n(S))\) 。其中,
- \(C_n(S)\) 是单纯 \(p\) 复形 \(S\) 的 \(n\)-chain group
- \(\mathscr C(S)\) 是单纯 \(p\) 复形 \(S\) 的链复形
由于 $$ \partial_{n}\partial_{n+1} = 0 $$ 因此: $$ \forall \sigma \in C_{n+1}(S): \partial_n(\partial_{n+1}(\sigma)) = 0 \newline \implies \partial_{n+1}(\sigma) \in \ker \partial_n \newline \implies \image\partial_{n+1} \subseteq \ker \partial_n $$ 从而,我们可以定义 \(n\) 阶同调群 \(H_n = \ker \partial_n / \Im \partial_{n+1}\)
- 其中,\(\ker \sigma_0 = \{0\}\)