Parsing¶

简单来说，直到 parsing 这一步，我们才涉及到 grammar，也就是需要在意上下文了。

关于 CFG、EBNF 格式这些东西，since they are trivial, they won't be discussed here.

推导和规约¶

定义¶

假如我们有产生式 $A \to \gamma$，那么可以有这样的变换：$\alpha A \beta \Rightarrow \alpha \gamma \beta$。我们可以说：

$\alpha A \beta$ 直接推导 (derive) 到 $\alpha\gamma\beta$
$\alpha\gamma\beta$ 直接规约 (reduce) 到 $\alpha A \beta$

不难看出：推导=从文法生成语言里的句子，规约=识别句子成分并逐渐规约到开始符号

最左推导和最右推导¶

最左推导=每步代换最左边的非终结符。逆过程为最右规约
类比可得出最右推导、最左规约的定义
在自顶向下的分析中，总是采用最左推导；在自底向上的分析中，总是采用最左归约

Parse Tree¶

分析树性质
- 根节点=文法初始符号
- 叶节点=终结符
- 内部节点=非终结符
- 父节点→{叶节点}=产生式
语法分析(Parsing)中的挑战
核心目标：对于终结符号串 x，要么从 S 推导出 x，要么设法将 x 规约到 S
- 自顶向下(Top-down) S->x, 从根节点开始构造Parse Tree
- 自底向上(Bottom-up) x->S, 从叶节点开始构造Parse Tree 作为搜索问题：搜索空间大->空间大小受文法产生式限制。
- 无限制文法：时间复杂度 $O(n^3)$
  - 可以想象：如果自底而上的话，最差情况下，需要将当前字符串 $s$ 的所有子串 $s[i:j]$ 遍历一遍，然后只能将 $s$ 的长度减小 1。从而，时间复杂度就是：$O(\sum_{i=1}^n \frac {i(i+1)} 2 + 1) = O(n^3)$
- 上下文无关语言 CFL 的子集需要的典型时间为 $O(n)$，例如
  - Predictive parsing using LL(1) grammars
  - Shift-Reduce parsing using LR(1) grammars
  - ……

Ambiguous Grammar¶

A good example

如果词法这样（摘自于 SysY 词法）：

Exp ::= AddExp;

MulExp ::= UnaryExp | MulExp ("*" | "/") UnaryExp;
AddExp ::= MulExp | AddExp ("+" | "-") MulExp;

UnaryExp ::= Number;

那么 2 / 2 * 5 + 3 只能是

E
|
A___
| \ \
A + M_
|     \
M___  U_
|\  \   \
M * U_  3
|     \
M / U 5
|   |
U   2
|
2

也就是：(((2 / 2) * 5) + 3)

A bad example

但是，假如说不讲章法，直接乱来：

Exp ::= Exp | Exp ('+' | '-' | '*' | '/') Exp | Number;

那么，((2 / (2 * 5)) + 3) 可以，(2 / (2 * (5 + 3))) 也可以。但是这两个都不符合四则运算的优先级。

从上面两个例子中，我们可以粗浅看出：如果希望将隐式的四则变量优先级，变成 EBNF 中显式的优先级，那么就必须要

加入更多 non-terminals (即 AddExp, MulExp 等等这些)
- 从而可以迫使一些 ?Exp 必须在另一些 ?Exp 之后才能被生成出来

可以证明，任意 CFG 的二义性是 undecidable 的。因此，我们需要使用 unambiguous grammars 来保证无二义性：

自顶向下：LL(1)
自底向上：LR(1), LALR(1)

Types of Parsers for Grammars¶

有三种：

Universal：可以适配任何 grammar，但是过于 inefficient
Top-Down (LL grammar, i.e. Left-to-right Leftmost-derivation)：从 root 到 leaves
Bottom-Up (LR grammar, i.e. Left-to-right Rightmost-derivation)：从 leaves 到 root

这种 Universal Parsing 是带回溯机制的，因此可想而知，处理起来基本上不可能是 $O(n)$。

不论是 TD 还是 BU，两者都是从左到右一个一个字符处理的，能够达到线性复杂度（想想看，对于巨型工程而言，$O(n^2)$ 完全不可接受）。因此能够识别的文法有限（LL 和 LR）。但是即便是这些文法的语法，也够我们用了。

至于 TD 和 BU 的区别：

TD 支持的 LL 文法类比 BU 的 LR 文法类更狭窄
我们可以手工实现 TD parser
但是只能用自动化工具生成 BU parser（比如 yacc、bison、menhir）

Top-Down Parsing¶

如上图：

首先，我们有一个 S，以及一个 begin print num
读入一个 token (begin)，我们发现只有 begin S L 能够匹配，因此 S -> begin S L，目前是 begin S L
读入一个 token (print)，我们发现只有 print E 能够匹配，因此 S -> print E，目前是 begin print E L
读入一个 token (num)，我们发现只有 num 能够匹配，因此 E -> num，目前是 begin print num L
读入一个 token (<EOF>)，我们发现只有 end := <EOF> 能够匹配，因此 L -> end := <EOF>，目前是 begin print num <EOF>

递归下降分析¶

Naive Parsing¶

如上图，我们把每一个非终结符抽象成一个函数（比如 L 这个非终结符就是 void L(void) 这个函数）

def parser(tokens = ['BEGIN', 'PRINT', 'NUM', '\0']):
    global getToken
    def getToken():
        try:
            cur_tok = next(getToken.get)
            return cur_tok
        except AttributeError:
            getToken.get = lexer()
            cur_tok = next(getToken.get)
            return cur_tok
    global li
    li = tokens
    try:
        S()
        try:
            getToken()
            raise Exception("parse failed") # not complete
        except:
            print("parse succeeded")
    except:
        raise Exception("parse failed") # can't parse

def L():
    advance()
    print(tok)
    if tok == "\0":
        eat("\0")
    elif tok == ";":
        eat(";")
        S()
        L()
    else:
        raise Exception()

def S():
    advance()
    print(tok)
    if tok == "IF":
        eat("IF")
        E()
        eat("THEN")
        S()
        eat("ELSE")
        S()
    elif tok == "BEGIN":
        eat("BEGIN")
        S()
        L()
    elif tok == "PRINT":
        eat("PRINT")
        E()
    else:
        raise Exception()

def E():
    advance()
    print(tok)
    if tok == "NUM":
        eat("NUM")
    else:
        raise Exception()

def eat(t):
    assert tok == t
    advance()

def advance():
    global tok
    tok = getToken()



def lexer():
    """
    这里简化成这样
    """
    for i in li:
        yield i
    yield None # 已经用尽了所有字符

Optimization: Predictive Parsing¶

Naive method 的问题

但是，上文没有考虑到需要回溯的情况：比如，我需要 parse 一个四则运算。那么：

假设第一个 token 是 NUM(114514)，那么我应该使用哪一条规则呢？
目前的非终结符是 S，因此只能是 S -> E$
然后，目前的非终结符是 E，可选项有 E -> E + T 和 E -> E - T。该选哪一个？我们根据目前信息无从下手。
因此，只能两个都试一遍，第一个成功就选第一个，否则试第二个。这就产生了分支
之后在每一个非终结符处，都可能会有分支，导致算法复杂度最差能达到指数级别

在产品级编译器中，parsing 时间占据大约 1/3，是耗时的大头，因此亟待优化。

一些定义¶

上面是 LL(1) 文法的。对于 LL(k) 文法，我们将 $t$ 定义为长度为 $k$ 的 terminal symbols 即可。

不难发现，对于字符集 $\Sigma$ 而言，LL(k) 文法的 $\operatorname{First}(\gamma)$ 里面可能有 $|\Sigma|^k$ 个元素，是指数级增长的

如何选择生成规则¶

要么：

$\gamma$ 能够某种推导中，第一个字母是 $t$
- $t$ 由 $X$ 生成出来
$\gamma$ 的够某种推导中，推导成 $\epsilon$ (即空串)，且 $S \rightarrow^\ast \beta Xt \delta$
- $t$ 由 $X$ 后面东西的生成出来，而 $X$ 本身是个空串

如何计算 Nullable, First 和 Follow¶

先把 nullable 推出来
- 至于手动推导的方法，其实不需要严格按照算法一步步推
然后把 first 推出来
最后把 follow 推出来

下面是（虎书中的）完整算法：

这里其实是在同步计算 nullable, first 和 follow 三者，和我们之前讲的逐个模块计算不同

如何得到 Predictive Parsing Table¶

“如何选择”一章已经说过：我们需要构造一个分别为 Next Token (T) 以及 Non-Terminal Symbols (X) 的表格（如上图左下角所示）。我们这里再重复一遍。

构造表格的规则

如果：

T 属于 First(gamma)，且 X -> gamma
或者，gamma is Nullable，且 T 属于 Follow(X)，且 X -> gamma

那么就将这个转换规则填入对应表格

构造完成之后，如果一个表格有超过一条规则，就是错误的。

比如，这个例子就是错误的，因为 (Z, d) 有两条规则
不过，对于一个更简单的例子——检测括号是否匹配——如果我们用 S -> (S) S; S -> eps，那么显然可以满足上述条件，因此检测括号这个确实是 LL(1)

反例以及修改¶

举一个简单的例子（T 是终结符）：

E -> E + T
E -> T

那么，显然，T, T + T, T + T + T 等等就属于这个语言。

但是，如果让我们做一张表：

	Nullable	first	follow
E	False	T	+

	+	T
E		E -> E + T E -> T

所以，T 有两条，重复了。那么，如何修改推导规则呢？我们可以改成：

E  -> T E'
E' -> + T E'
E' -> \epsilon

	Nullable	first	follow
E	False	T	+
E'	True	+

	+	T	$\varepsilon$
E		T -> T E'
E'	E' -> + T E'		E' -> \epsilon

这样就没有问题了。

如何将某些文法修改成符合 LL(1) 的¶

Info

下面的 a, b, c 等等，可以是单个字符，也可以是字符串。

比如，E -> E + T 中，a 就是 + T

立即左递归¶

对于

A -> Aa
A -> b
A -> c

这样的立即左递归 (immediate left recursion) 文法（其实就是对应语言 b, ba, bc, baa, bac, bca, bcc, baaa, baac, ...），我们可以直接改成立即右递归文法

A  -> bA'
A  -> cA'

A' -> aA'
A' -> \epsilon

从而得到满足 LL(1) 的文法。

例子：四则运算

如上图，我们把所有左递归形式（即 T -> T <op> F 以及 E -> E <op> T），都改成了右递归形式。这样就将四则运算的文法改成了 LL(1)。

然后，根据上面改后的文法，我们可以得到驱动表（请忽略图中那个红点~）：

Limitation

上面举的例子，可以处理所有立即左递归。但是对于非立即左递归（i.e. 通用左递归），就要用更高级的办法了。

Left Factoring¶

如果两个推导式之间有公共前缀的话，那么也会导致驱动表中的重复问题。

Error Recovery¶

如果我们遇到了语法错误——也就是说，上述规则都不适用了——那么我们最好能够在输出这个错误之后，从错误恢复过来，然后继续执行下去。

否则，在现实中，一次编译只输出一个错误，那么用户就需要编译很多遍，才能把错误都改完，造成很大不便

以 (1++1) * 3+2) 这个包含两个错误的地方，如果按照上面的驱动表来做的话，就是这样 S -> E$ -> T E'$ -> F T' E'$ -> (E) T' E'$ ->* (id T' E') T' E'$ ->* (id + T E') T' E'$ -> <stuck>。目前，我们有两个选择：

增加字符，直到能够继续运作。比如增加一个 id 之类的。但是，问题在于：第一，增加什么字符；第二，如何保证停机
减少字符，直到能够继续运作。比如减少 +。好处就在于必然可以停机

总结¶

我们可以为简单的编程语言（LL(K)），手工设计一个 top-down parser，以线性时间复杂度进行 parsing 以及 error correction。

Bottom-Up Parsing¶

相比 LL(k) 强大之处：

不是只看前 k 个 token 就做选择，而是看到整个产生式右部之后再做选择
- 也就是将 make decision 的时机推迟到了 entire right-hand side
- 最关键的问题，就是确定这个“时机”——我应该在什么时候去做选择

例子¶

具体过程如下：

. 代表目前 parser 到达的位置
对于下图右边的表格，左侧是一个栈（因此修改只能在最右侧进行），右侧是我们当前的状态

在 parse 的过程中，我们需要记录：

当前读入位置（也就是上图右表右侧的 .）
记录了 terminal 以及 non-terminal 的栈（也就是上图右表左侧的一堆东西）

Parser 可以有三种 actions：

shift: 将下一个字符 push 到栈里面
reduce R (e.g. 上图右表的 line 5 -> line 6):
- 栈顶需要 match RHS of some rule (e.g. T -> int * T)
- 将 RHS 推出栈 (e.g. pop int * T)
- 将 LHS 推入栈 (e.g. push T)
accept: shift $ (e.g. push $) and can reduce what remains on stack to start symbol (e.g. pop E $; push S)

LR(0) Parsing¶

就是无需看任何输入中的 token，只需要根据栈中的符号来确定是否进行规约。

也就是说：我们要设计的算法，只需要看栈的状态，就能决定在什么时刻进行 reduce，而根本不需要 look ahead。

我们的算法就是：

能 shift 就尽量 shift
假设本次 shift 会导致栈顶若干元素根本通过任何一条规则规约，那么才考虑 reduce

例子¶

S' -> S $
S  -> (S)
S  -> a

如上图：

. 就是当前 parser 的位置
a -> b . c 被称为 LR(0) items。就是我目前有了 b，只要你再给我生成一个 c，我就能产生一个 a

状态转移：

如果要实现前面的状态，那么必须实现后面的状态
- i.e. 后面状态是前面状态的必要条件
因此，有三种状态转移
- 第一种，$\varepsilon$
- 第二种，终结符。从输入中读取一个非终结符。
- 第三种，非终结符。实际上，输入中是不可能有非终结符的。我们这里是从左侧

转成 DFA 之后，如下图所示：

更简单的转换方法¶

实际上，由于这个 NFA 实际上是 $\varepsilon$-DFA（i.e. 在 DFA 的基础上，允许 $\varepsilon$ 边；或者说，在 NFA 的基础上，不允许重复的非 $\varepsilon$ 边），因此我们可以用更简单的转换方法：

如上图：

Closure 相当于把一个状态 ($I$) 以及从这个状态出发，无需消耗任何字符（i.e. 经过 $\varepsilon$ 边）即可达的状态都包含到大状态中
Goto 返回从这个状态出发，消耗 $X$ 这个字符即可达的大状态
- 别忘了 Closure(J) 的 Closure!
最后我们不断迭代，即可求出 E 和 T

例子¶

如上上表和上表：

分为三种状态
- 13589 状态：我们无脑选择 shift
  - 以上上表第二行为例：我们目前在 3 状态，就无脑先 shift。如果下一个字符是 x，就根据上表跳转到 2 状态去；如果下一个字符是 ,，就是 error。等等。
- 278 状态：无脑 reduce+goto
  - 以上上表第八行为例：我们目前在 6 状态，就无脑 reduce。由于规则里是 r1，因此就用第一条规则（i.e. S -> (L)）来 reduce，暂时来到状态 3；之后，我们获得了 S，因此 goto 状态 7
- 4 状态：无脑 accept
  - 就是第九行
概念上来说，分为状态栈和符号栈。实际上，每一个符号就对应一个状态，状态栈就应该比符号栈多一个初始状态（e.g. 上面的 1）而已。因此，状态栈和符号栈实际上可以用同一个 pair 栈来存

反例¶

如上图，状态 3 在下一个字符为 + 的时候，既可以 reduct+goto 也可以 shift，因此用 LR(0) 无法解决了。

但是，不难觉察到：如果你要应用规则 2 来 reduce 的话，首先，reduce 之后，会产生一个 E。因此，你起码必须保证，E+ 这种情况是存在的

换句话说，如果 + 不属于 FOLLOW(E) 的话，那么此时 E 根本不应该被 reduce 成 +

经过计算：FOLLOW(E) = {$}。因此，r2 只能存在于 [3, $] 这个格子中。也就是下图：

Simple LR (SLR) parsing¶

如上图，我们将 LR(0) 的算法计算出来的表格进一步简化，从而得到 SLR 表格。这就是 simple 的意思。

LR(1) parsing¶

LR(1) parsing比简单 LR（SLR）parsing 更强大。

LR(0)：仅根据当前状态来选择 shift 或者 reduce。
SLR：根据更多信息（下一个 token 是否在特定的 FOLLOW set 中）来选择 shift 或 reduce。

但是，即便是 SLR，仍然免不了 conflict（如下图）

反例

如下图：红框内的状态中，既可以 shift，也可以 reduce。而且 S -> V.=E 这条规则，确实满足要求（i.e. $= \ \in \text{Follow}(E) = \{\$, =\}$）

因此我，我们需要使用更多的信息。对于 LR(1) 而言，就是往 DFA 中加入更多信息。

回忆：LR(0) item 就是形如 $(A \to \alpha.\beta)$ 这样的。

LR(1) item 包含一个 LR(0) item 以及一个 lookahead symbol: $(A \to \alpha.\beta, x)$。

回忆：$(A \to \alpha.\beta)$ 的意思是：$\alpha$ 位于符号栈栈顶，剩余字符（的前缀）可以推出 $\beta$

$(A \to \alpha.\beta, x)$：$\alpha$ 位于符号栈栈顶，剩余字符（的前缀）可以推出 $\beta x$

回忆：SLR 中，对于规则 $A \to \alpha$，只有在 $X \in \text{Follow}(A)$ 的情况下，才能使用

对于 $(A \to \alpha.\beta, x)$ 而言，由于 $\text{First}(\beta x) \neq \emptyset$，因此我们可以直接说：只有在 $X \in \text{First}(\beta x)$ 的时候才能用。

实际上，SLR 和 LR(1) 都采取了 track the lookahead symbol 的措施。但是，对于规则 $A \to \alpha$，
- SLR 用的是 Follow($A$)，也就是粗粒度的 $A$，而且是在已经推导完 DFA 之后才加入这个限制
- 而 LR(1) 用的是细粒度的 First($\beta x$)，并将这个限制引入到推导 DFA 这个过程中去

推导过程¶

这里我们采用对比的方式进行讲解。

Closure¶

如上图：

start state 的 ? 的意思就是：由于 $ 已经是终止符了，因此我们根本不关心 $ 右边是什么符号（i.e. 直接 accept）
对于规则 $(A \to \alpha.X\beta, z)$ 而言，我们要求能够推出 $X\beta z$。因此，$X$ 也得能够推出 $\gamma$ + First($\beta z$) 才行。

Goto¶

其实没有变化。

Reduce¶

相比 SLR 而言，LR(1) 更加精确。

例子¶

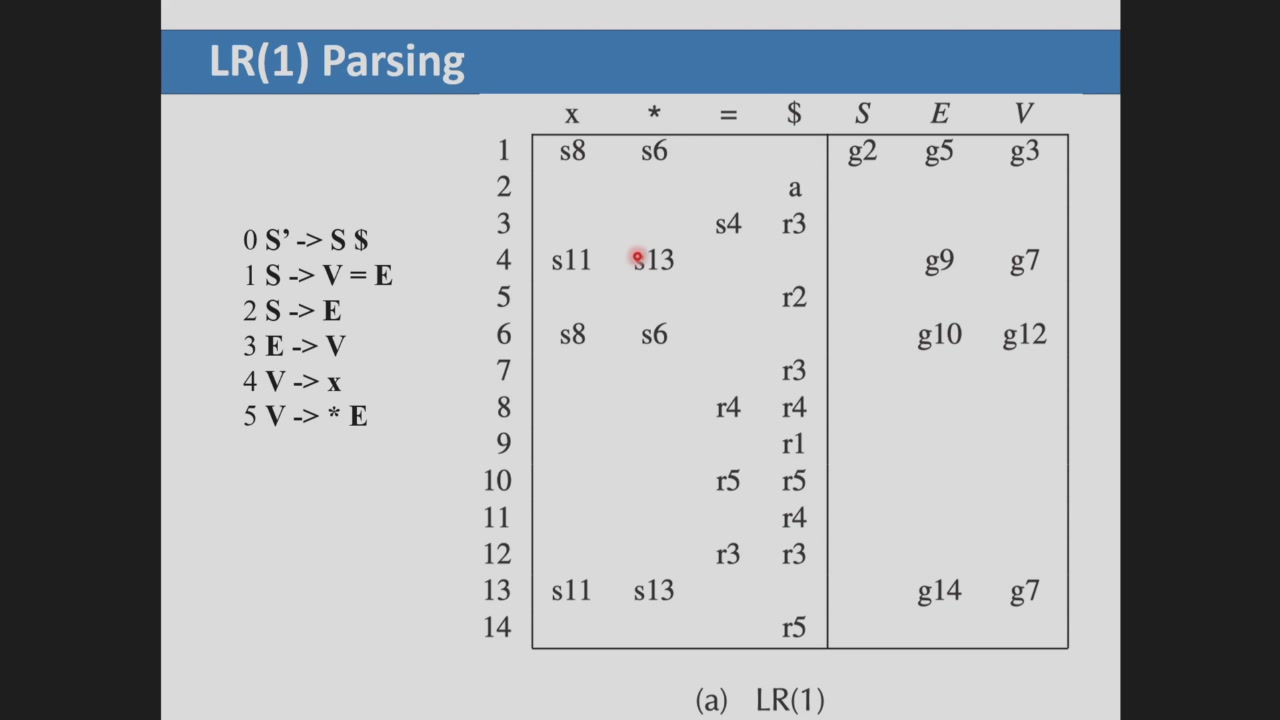
注意：对于上表中第三行，可见我们通过 LR(1) 这种更加细粒度的 DFA 构建，将 s4 和 r3 成功分开了。

LALR(1)¶

由于 LR(1) 可能对每一个 lookahead symbol 都要维护一个状态，因此当 lookahead symbol 很多的时候，这个表可能会很大。

因此，我们可以尝试把一些 states whose items are identical except for lookahead sets 合并起来，如下图：

Example

A Hierarchy of Complexity¶

LR Parsing of Ambiguous Grammars¶

我们用最简单的例子进行说明（dangling else）。

如图，大部分语言都会使用 else 就近原则——也就是说，(1) 是正确结果。所以，我们怎样能够正确 parse 这个 dangling else 呢？以下是两种解法。

改写语法¶

如上图：U -> if E then M else U 这一条规则，就是说，如果你需要匹配一个完整的 if then else（i.e. 最后的 else 和最前面的 if 绑定），那么中间的 then 内部就必须是全部完整的。

使用 priority¶

还记得我们之前说的吗？能够 shift 就 shift，不能 shift 才考虑 reduce。

因此，如果 shift 和 reduce 规则冲突，那么我们就 shift。

更广义来说，如果产生了 conflict，我们其实可以通过手动规定优先级的方式，去消除这个 conflict。

Warning

但是，除了一些特殊的例子（比如说这个 dangling else）以外，出现其它的 shift-reduce conflict 或者 reduce-reduce conflict，都意味着你的文法有问题

Error Recovery¶

Local Error Recovery¶

如上图：左侧蓝框内，蓝色规则（i.e. 最下面两条规则）就用于 error recovery。

如果产生了 error，那么：

我们需要不断 pop symbol stack，直到满足 error 的左侧
不断 discard new input，直到满足 error 的右侧

问题¶

如上图：

文法匹配若干以分号相隔的含括号的表达式
生成 error 之后，它需要
- 左边匹配一个 ;
- 右边匹配一个 ;

如果在读取若干左括号之后，出现了 error，那么就会先左边 pop，把左括号删掉，然后再右边 discard，把右括号删掉。

但是，由于左括号已经导致了 nest = nest + 1 这个副作用，而右括号在导致 nest = nest - 1 之前已经被 discarded，因此，最终输出就是 nest 不为 0。

解决方法：我们最好不要用有副作用的 semantic action。

除此之外，另外一个问题就是：local error recovery 只能够局部删除/修改。

以上图为例：肉眼可见，错误其实来源于 var 被错误写成了 type。

但是，由于出错的地方在 :=，因此，修改错误的时候：

要么是用上面所说的“删除式修改”，即把 type ... of 0 全部都删了。这样会导致错误信息不够清晰
即便用“修改式删除”，如果把 := 改成了 =，在后面的 intArray[10] 这里也会出问题。因为 type 后面是不能接 [...] 的

因此，只有用全局修改，我们才能直接将错误根源 type 找出来、

Global Error Recovery¶

目的：通过最少的插入/删除操作集合，将语法错误的输入修改成语法正确的输入（从而，即便“真正出错”的位置并不是 parsing 阶段报错的位置，我们也一定程度上可以通过这种 global 的方式找出来）

Burke-Fisher Error Repair (back up $k$ tokens)¶

除了正常的符号栈（这里称为 current stack）以外，我们还额外维护一个 old stack 以及 queue：

这个 queue 的长度就是 k
old stack + queue = current stack

每当我们遇到错误之后，我们就轮流对这个 queue 中的所有可能的位置进行deletion/insertion/substitution 三种操作。只要找到一种位置+方式，使得我们可以成功往前 parse $r$ 个 tokens 以上，我们就采用这种位置+方式。

	+	T	\(\varepsilon\)
E		T -> T E'
E'	E' -> + T E'		E' -> \epsilon

Parsing¶

推导和规约¶

定义¶

最左推导和最右推导¶

Parse Tree¶

Ambiguous Grammar¶

Types of Parsers for Grammars¶

Top-Down Parsing¶

递归下降分析¶

Naive Parsing¶

Optimization: Predictive Parsing¶

一些定义¶

如何选择生成规则¶

如何计算 Nullable, First 和 Follow¶

如何得到 Predictive Parsing Table¶

反例以及修改¶

如何将某些文法修改成符合 LL(1) 的¶

立即左递归¶

Left Factoring¶

Error Recovery¶

总结¶

Bottom-Up Parsing¶

例子¶

LR(0) Parsing¶

例子¶

更简单的转换方法¶

例子¶

反例¶

Simple LR (SLR) parsing¶

LR(1) parsing¶

推导过程¶

Closure¶

Goto¶

Reduce¶

例子¶

LALR(1)¶

A Hierarchy of Complexity¶

LR Parsing of Ambiguous Grammars¶

改写语法¶

使用 priority¶

Error Recovery¶

Local Error Recovery¶

问题¶

Global Error Recovery¶

Burke-Fisher Error Repair (back up \(k\) tokens)¶