Skip to content

Lec 4: Floating Points

Before 1985, there wasn't a universal representation of floating point numbers. So one program working on one machine might not be working on another.

IEEE Standard 754

The IEEE 754 Floating Point Representation is shown below:

     1 bit            8 bits              23 bits
+--------------+------------------+-----------------------+
|     Sign     |     Exponent     |       Mantissa        |
+--------------+------------------+-----------------------+

Here, the number represented is $$ (-1)^{S}M2^{E} $$ where normally, \(M \in [1.0, 2.0)\).

And, in the representation

  • \(S\) = sign field
  • exp field encodes E (but is not equal to E)
  • frac field encodes M (but is not equal to M)

Precise Implementation for IEEE 754

Form \(Exponent\) \(Mantissa\) Value
Zero \(0\) \(0\) \(0\)
Denormalized Form \(0\) non-\(0\) \((-1)^{Sgn}2^{-126}(0.Man)\)
Normalized Form \(1\sim254\) arbitrary \((-1)^{Sgn}2^{Exp - 127}(1.Man)\)
Infinity \(255\) \(0\) \(\infty\)
NaN \(255\) non-\(0\) NaN

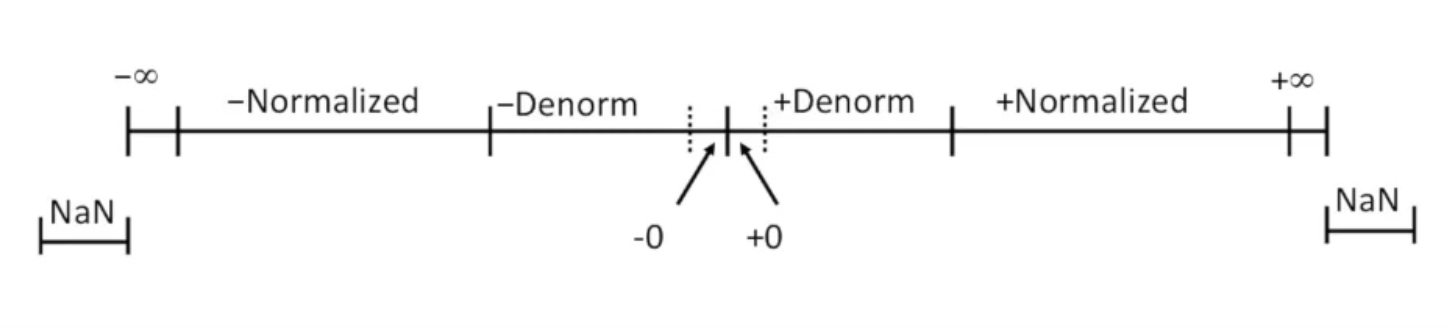
Visualization:

image-20240108230832218

Some Variations of IEEE 754

  • Single Precision: (1, 8, 23) ------------------------------> 32 bits
  • Double Precision: (1, 11, 52) --------------------------> 64 bits
  • Extended Precision (Intel only) : (1, 15, 63/64) --> 79/80 bits

... and also a generic definition of the forms

Form \(Exponent\) \(Mantissa\) Value
Zero \(0\) \(0\) \(0\)
Denormalized Form \(0\) non-\(0\) \((-1)^{Sgn}2^{1-Bias}(0.Man)\)
Normalized Form \(1\sim 2^{\#E}-2\) arbitrary \((-1)^{Sgn}2^{Exp - Bias}(1.Man)\)
Infinity \(2^{\#E}-1\) \(0\) \(\infty\)
NaN \(2^{\#E}-1\) non-\(0\) NaN

where usually \(Bias = 2^{\#E-1} - 1\).

  • In the case of IEEE 754, \(Bias = 2^{8 - 1} - 1 = 128 - 1 = 127\).

Distribution of Floating Point Numbers

Take (1,3,2) as example.

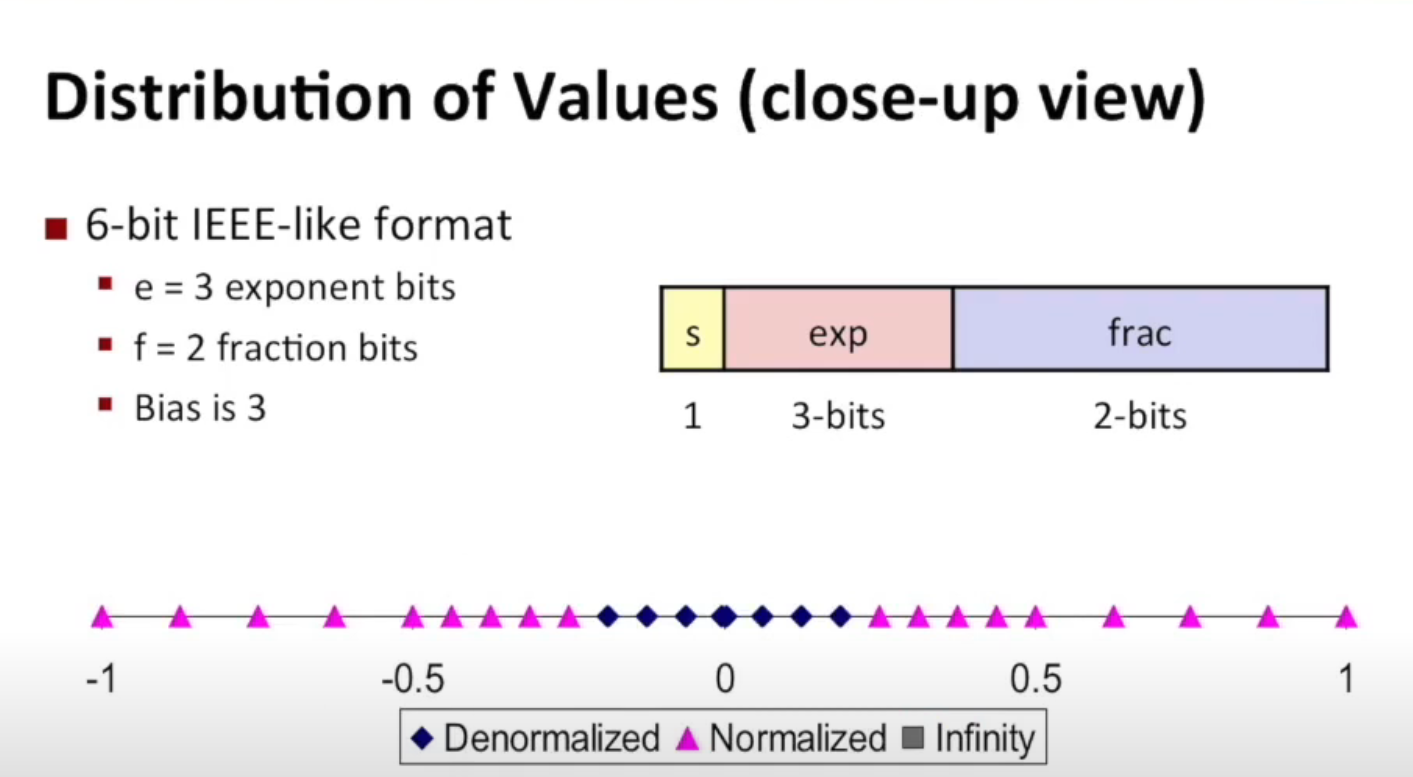
image-20240108232715036image-20240108232728507

One can observe the presence of uniformly distributed values close to zero. Additionally, a step-like pattern of uniformly distributed values is apparent when examining normalized values.

Properties of the IEEE encoding

  • FP Zero is the same as Integer Zero
  • i.e. All bits = 0
  • Can (Almost) Use Unsigned Integer Comparison
  • Must first compare sign bits
  • Must consider -0 =0
  • NaNs problematic
    • Will be greater than any other values
    • What should comparison yield?
  • Otherwise OK
    • e.g. Denorm vs.normalized Normalized vs.infinity

Operations on FP

Basic Idea

First, compute the exact result.

  • Assuming you have infinite amount of bits available

Next,

  • make it infinity if it's too large.
  • round it if it's too long

Rounding

There are four major ways of rounding.

Value Towards zero Round down (\(-\infty\)) Round up (\(+\infty\)) Nearest Even (default)
$1.40 $1 $1 $2 $1
$1.60 $1 $1 $2 $2
$1.50 $1 $1 $2 $2
$2.50 $2 $2 $3 $2
$-1.50 -$1 -$2 -$1 -$2

"Nearest Even" is used in IEEE standard. But you can choose the way you round in assembly code.

How To Round?

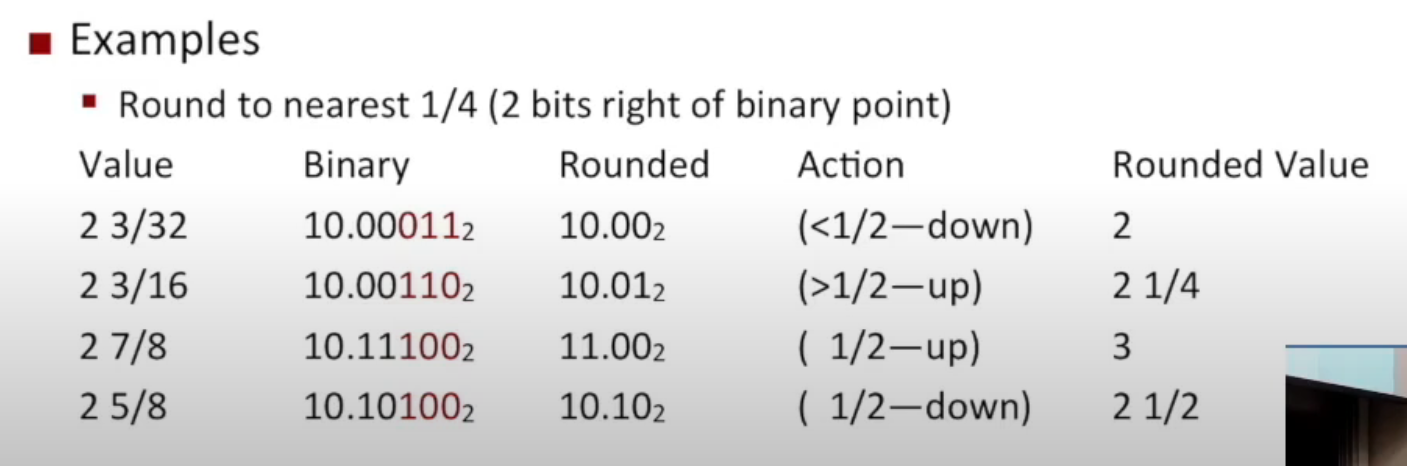
image-20240109010445555

If the digits to be truncated is

  • greater than 1/2: Round UP!
  • smaller than 1/2: Round DOWN!
  • equal to 1/2: Round EVEN!
ROUND_TO_EVEN (x_x0.x1_x2_..._xn)
    IF (x1 & (!x2_..._xn)) BEGIN
        x_x0 := x_x0 + x1
    END ELSE BEGIN
        // x1_x2_..._xn == 10...0
        x_x0 := x_x0 + x0;
    END
ENDFUNCTION

Multiplication

  • $ (-1)^{s_1} M_1 2^{E_1} \times (-1)^{s_2} M_2 2^{E_2} $

  • Exact Result: $ (-1)^s M 2^E $

  • Sign s: \(s_1 \oplus s_2\)

  • Significand M: \(M_1 \times M_2\)

  • Exponent E: \(E_1 + E_2\)

  • Fixing

  • If \(M \geq 2\), shift M right, increment E

    • note that both \(M_1, M_2 \in [1.0, 2.0)\), so their product must be smaller than \(4.0\).

  • If E is out of range, overflow

  • Round M to fit fractional precision

  • Implementation

  • The biggest chore is multiplying significands.

Addition

image-20240109012556103

Mathematical Properties of FP Add and Mul

image-20240109013849582image-20240109013911544

Tip:

  • In nature, things change smoothly. So you seldom run into the problem of non-associativity.
  • But in some fields, e.g financial market, the indices vary dramatically. So you might run into problem, if you use default FP representation.

FP in C

C guarantees two levels

  • float: "single precision"
  • double: "double precision"

Casting (between int, float, and double)

  • int \(\to\) double: No rounding needed
  • int \(\to\) float: As float only has mantissa of 23 bits, it might round according to a certain rule.
  • float/double
  • truncate fractional part
    • i.e. round to zero
  • not defined when out of range or NaN, but usually to TMin (i.e. \(-2147483648\))