Sequence-to-Sequence with RNNs

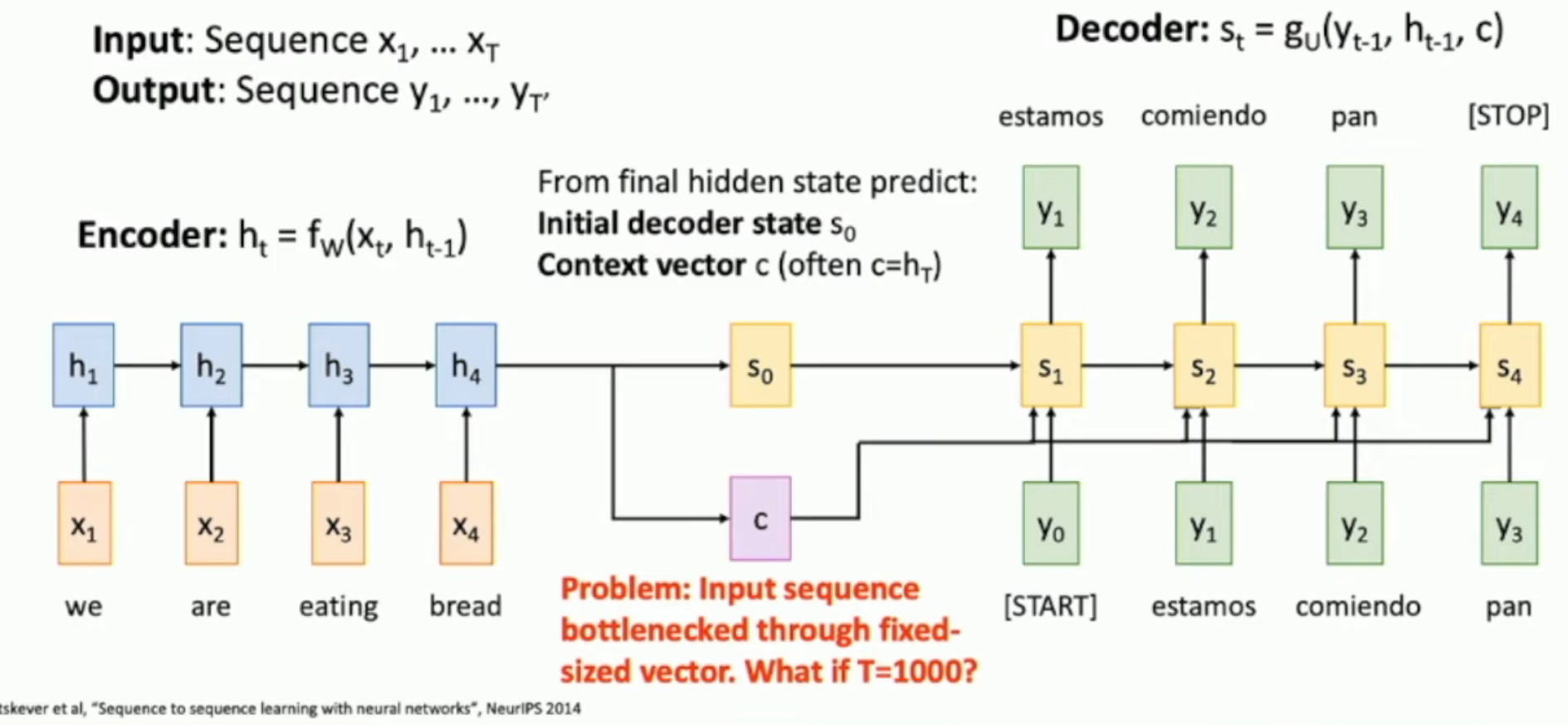
如图，对于 sequence to sequence（两者不一定对齐/等长）的文本转换，我们如果使用传统 RNN 架构，就如上图所示：

• 把所有关于原文的信息封装在 \(c\) 和 \(s_0\) 里面

可惜，\(c\) 的长度有限，直觉上+信息论上并不能够封装任意长的信息。因此，我们需要的是充分利用到每一个 \(h_i\)。

Attention Mechanism

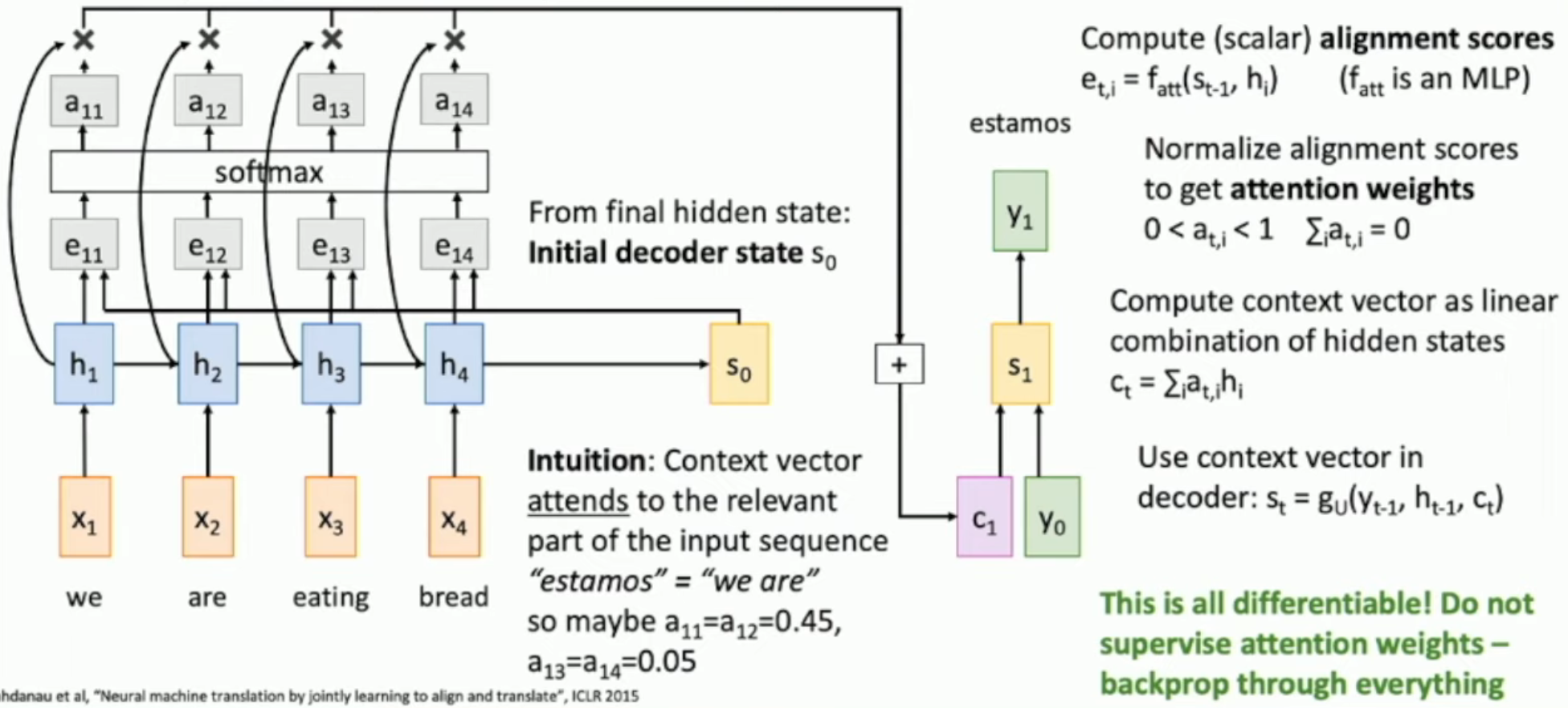
如图，我们的 idea 是：

1. 生成每一个词的时候，都让上一个状态来决定我们的对 \(h_1 \sim h_T\)​ 的 attention
   • i.e. \(e_{t,i} = f_{att{(s_{t-1}, h_i)}}\)，第 \(t\) 轮生成词语时，对第 \(i\) 个文本词语的 attention 就是 \(e_{t,i}\)
2. 然后，我们通过该轮的 attention vector，加权平均得到 context vector，从而生成我们本轮的状态

比如：直觉上来说，"estamos" 在西语中，意思是 "we are"，因此，对 "we" "are" 的 attention 应该差不多多，而对 "eating" "bread" 的 attention 也应该差不多少。

• 从而，我们既能够利用上所有的 \(h_i\)（i.e. 文本信息），也能够保证使用的合理性（i.e. 不是只取特定的 hidden state vector，而是根据需要来取用某一些 vectors。这和实际的语言翻译等工作是类似的）

Interpretability

如图，我们可以通过 attention 的矩阵，直接解读出哪些词语和哪些词语之间有关系——"European Economic Area" 和 "zone économique européenne" 是一一对应但是倒序的关系。

Observation: set not a sequence

这样的 naïve attention mechanism 并没有考虑到输入文本是一个 ordered sequence，而只是把输入文本当成了 unordered set。

• 作为对比，\(s_{t-1}\) 是一个 hidden state vector，intrinsically 考虑了临近性——i.e. 它大概只会“记录”附近的一些向量。但是通过 \(f_{att}\) 生成 \(e_{t,i}\) 的时候，却对于所有 \(h_i\) 一视同仁，而非更加注重某一些“更可能更有价值”的 \(h_i\)。

因此，attention mechanisn 可以使用于任何的 input，不论有没有序，比如图像等等。

Attention: Image2Caption

Recap: 我们之前的 image to caption via RNN 的方式，是将所有的 CNN 输出作为变量 \(\vec v\)，输入到 RNN 中，

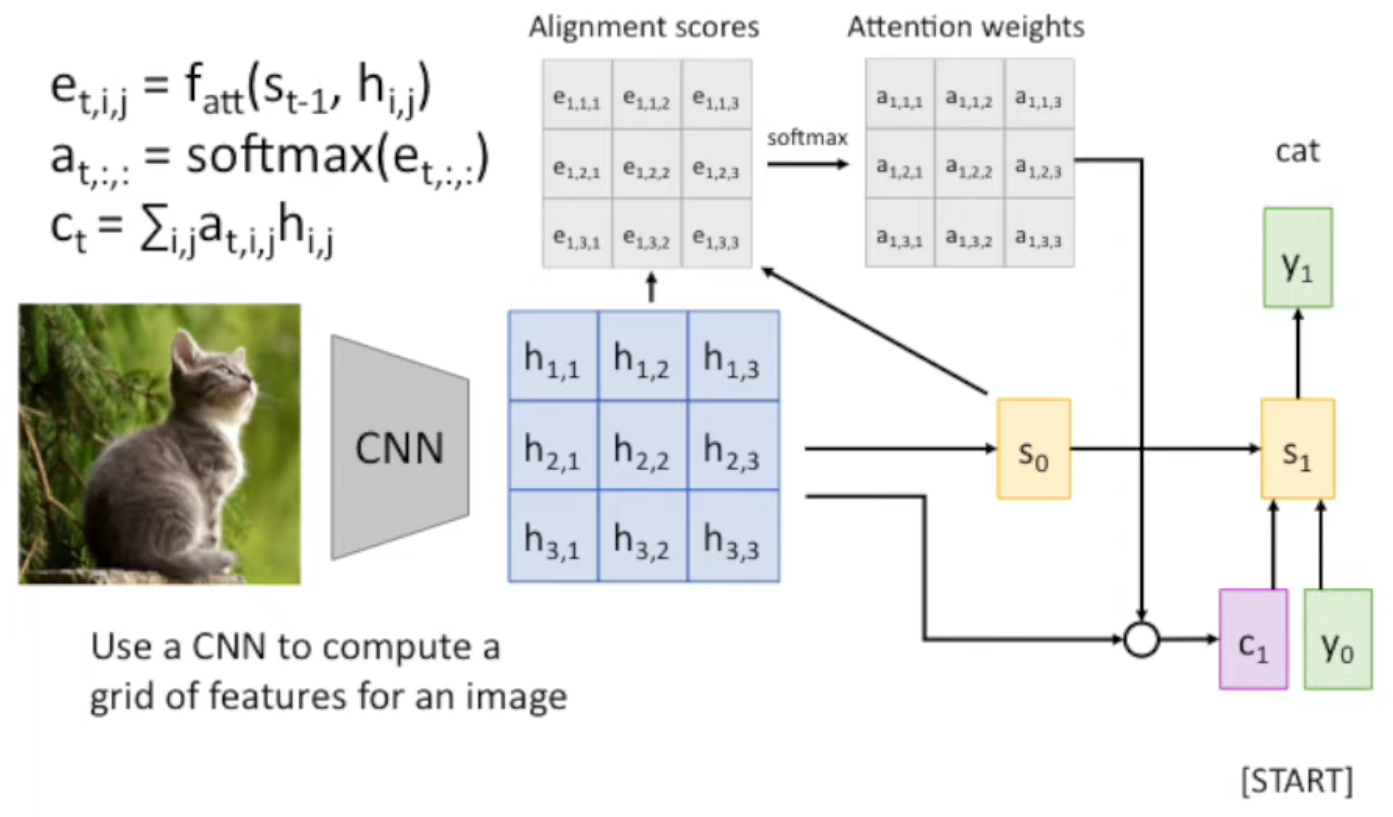
与之前的方法对比，我们之前是将整个 CNN 的输出作为变量 \(\vec v\)。而现在，我们是：

• 首先通过 CNN feature vector and previous state，生成 alignment scores
• 对 attention vector 进行 softmax 归一化，生成 attention weights
• 通过 attention weights 对 CNN feature vector 做加权平均，生成 \(c_n\)
  • \(c_n\) 和 \(h_{i,j}\) 的形状是一样的。如果 \(h_{i,j}\) 是 vector，那么 \(c_n\) 也是；如果 \(h_{i,j}\) 是 scalar，那么同理
• 最后，才将 \(c_n\) （而不是 \(\vec v\)）作为其中一个变量输入到函数中，生成 current state

Example

Biological Background

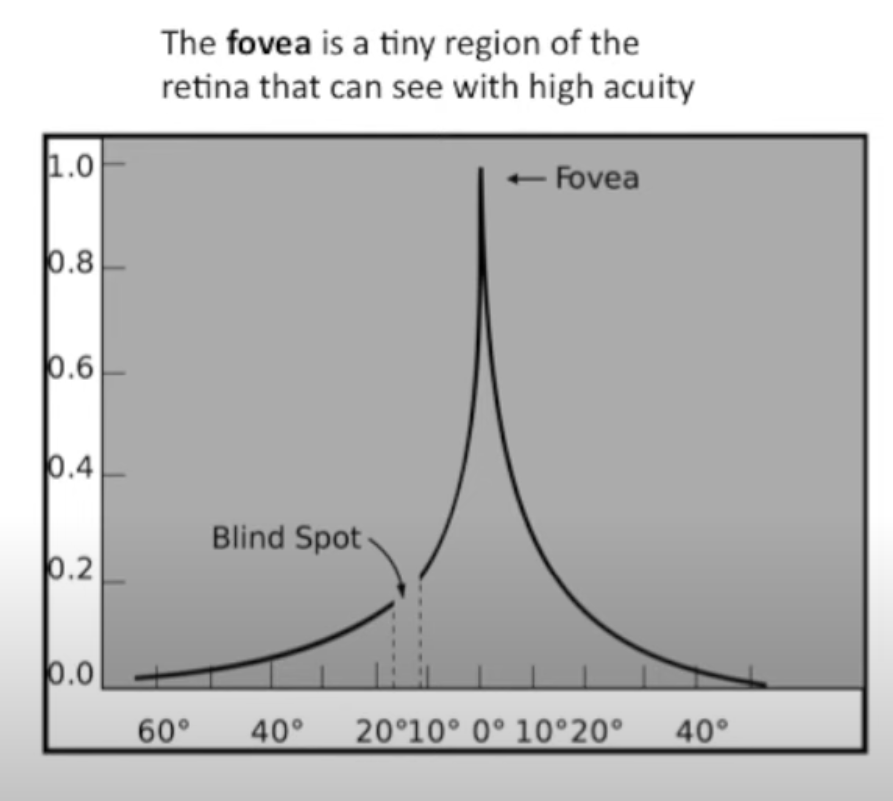
如图，只有视网膜黄斑附近的 visual acuity 最高，因此我们看东西的时候，会进行频繁的 saccade (眼跳动，也就是眼球转动)，从而获得更多的信息。Attention 机制就是在模仿这种 saccade。

When To Use Attention?

If you want to

• convert one type of data into another type of data
• do it over time (i.e. one step at a time)

you can often use some kind of attention mechanism to cause the model to focus on different chunks/parts of input while generating each part of the output.

Generalized Attention Mechanism

First Generalization

相比我们之前使用的 attention mechanism

• 这里使用 scaled dot product 当作 \(f_{att}\)
  • 为何需要 scale？因为 softmax 并不是 linear 的。\(20, 40\) 之间差了 \(e^{20}\)，而 \(2, 4\) 之间只差了 \(e^2\)
  • 另外，我们也避免使用神经网络这样复杂的结构来作为 \(f_{att}\)​​，简化了运算
  • 具体 scale 的原因，可以认为，这样能够让 \(\operatorname*{Var}(e_i - e_j)\)​ 在维数增加的时候，保持不变
    • 详见：StackOverflow
• 最终结果是：\(ans = X^t \operatorname*{softmax}(Xq/\sqrt{D_Q})\)​
  • 其中，最后一行的 "(Shape: D_x)" 就是 D_Q

Second Generalization

首先，上面一行只有 1 个 query。我们难道不能用多个 queries 吗？

也就是 $$ ans = X^t \operatorname*{softmax}(XQ/\sqrt{D_Q}, \dim=0) $$

• 其中，\(\dim=0\) 的意思就是：在行数变化的方向上，进行 softmax，也就是一列一列地 softmax。其中，每一列，就是我们一个 query 生成的 alignment scores
• e.g. 对于一个 9×9 的图片，
  • 此处需要 reshape 为 27×3
  • 然后，我们可以使用长度为 3 的 query，并且一次使用 9 个 queries，形成 3×9 的矩阵 \(Q\) ，
  • 再和 \(X\) 相乘为 27×9 的 matrix of alignment scores（相乘之后要除以 \(\sqrt{D_Q} := \sqrt{3}\)）
  • 然后，再 softmax，形状不变，称为 matrix of weights
  • 最后，与 \(X^t\) 相乘，就是 3×9 的 matrix of weighted picture
• 可以发现，matrix of queries 和 matrix of weighted pictures 的形状一样

Third Generalization

如上所示，相比 second generalization，我们增加了 K 和 V，而不是让 X 直接与 E、A 接触。

• i.e. 去掉上图中的 V 和 K，就是 second generalization；加上 V 和 K，就是 third generalization。

Variation: Self-Attention Layer

如上图所示，self-attention 不过不使用 query vector，而是把 input vector 经过 query matrix 当作 query vector。

不过，self-attention layer 有这样的性质：给定任意的 permutation matrix \(P\)，都有 \(\operatorname*{self-attention}(PX) = P \cdot \operatorname*{self-attention}(X)\)。也就是说，self-attention layer 不考虑顺序。

• 从而，如果你希望让它考虑顺序，就要人为 encode 进去。

Variation: Masked Self-Attention Layer

如图，为了防止之前的预测使用之后的预测结果（关键是我们根本不知道），我们需要人为加上 mask。